如图.△ABC内接于⊙O.D.F分别是$\widehat{AC}$与$\widehat{AB}$上的点.$\widehat{BF}$=$\widehat{DA}$.连接AF并延长交CB的延长线于点E.连接AD.CD.求证:△CDA∽△ABE．题目和参考答案——青夏教育精英家教网——

题目内容

7．

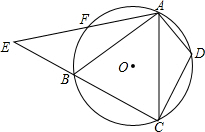如图，△ABC内接于⊙O，D，F分别是$\widehat{AC}$与$\widehat{AB}$上的点，$\widehat{BF}$=$\widehat{DA}$，连接AF并延长交CB的延长线于点E，连接AD，CD，求证：△CDA∽△ABE．

分析根据圆周角定理得到∠BAF=∠ACD，根据圆内接四边形的性质得到∠ABE=∠D，则根据有两组角对应相等的两个三角形相似即可得到结论．

解答证明：∵$\widehat{BF}$=$\widehat{DA}$，
∴∠BAF=∠ACD，
∵∠ABE=∠D，
∴△CDA∽△ABE．

点评本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似；有两组角对应相等的两个三角形相似．也考查了圆周角定理．

练习册系列答案

萌齐小升初强化模拟训练系列答案

小升初全能卷系列答案

小升初全优模拟大考卷系列答案

考试先锋小升初全真模拟试卷系列答案

小升初衔接教材系列答案

学业水平总复习系列答案

毕业升学总动员系列答案

日练周测新语思英语系列答案

全优中考系统总复习系列答案

全优卷练考通系列答案

相关题目

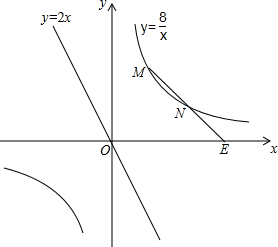某数学兴趣小组的同学再一次探究中发现：若平面直角坐标系中有两点A（x₁，y₁）和B（x₂，y₂），则线段AB的中点C的坐标为（$\frac{{{x_1}+{x_2}}}{2}，\frac{{{y_1}+{y_2}}}{2}$）．经过进一步的讨论，他们呢借助中位线和一次函数的知识证明了这一结论，请你使用该结论解答下面问题．
（1）若平面直角坐标系中有两点D（5，2）和E（-1，-4），则线段DE的中点F的坐标为（2，-1）；
（2）如图，点M是双曲线y=$\frac{8}{x}$在第一象限内的分支上的一点，点K的坐标为（6，0），线段MK的中点N也在这一分支上，则点M的坐标为（2，4），点N的坐标为（4，2）；
（3）在（2）的条件下，设点P为x轴上的一点，点Q为直线y=-2x上一点，若以M、N、P、Q为顶点的四边形是平行四边形，试求点P和点Q的坐标．

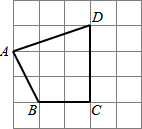如图所示的方格中，每一小格是一个边长为1厘米的小正方形，求四边形ABCD的面积和周长．

已知：如图．
（1）如果$\frac{AE}{AC}$=$\frac{AD}{AB}$，那么$\frac{AE}{CE}$=$\frac{AD}{BD}$吗？为什么？
（2）如果$\frac{AB}{BD}$=$\frac{AC}{CE}$，那么$\frac{AB}{AD}$=$\frac{AC}{AE}$吗？为什么？

2．若a²=（-2）²，则a等于（　　）

12．-5.8是5，8的相反数；+3的相反数是-（+3）；-$\frac{1}{2}a$的相反数是$\frac{1}{2}$a．

19．关于函数y=（500-10x）（40+x），下列说法不正确的是（　　）

y是x的二次函数

二次项系数是-10

一次项是100

常数项是20000

16．数字1，2，3，4，5，每个数字仅用1次，用学过的运算法则使它得结果等于999．你的一种算法是：5³×2×4-1=999．

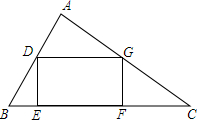如图，已知△ABC中，BC=24，在△ABC中截出一个矩形DEFG，已知矩形的面积S与EF的长x满足关系式：S=-$\frac{2}{3}$x²+16x，问：EF的长为多少时，矩形的面积等于72？