题目内容
18.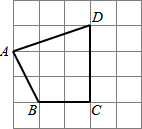 如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积和周长.
如图所示的方格中,每一小格是一个边长为1厘米的小正方形,求四边形ABCD的面积和周长.
分析 作AE⊥CD于E,由四边形ABCD的面积=△ADE的面积+梯形ABCE的面积,列式计算即可求出面积;根据勾股定理求得AB、DA的长,根据周长的定义即可求出四边形ABCD的周长.
解答  解:如图,作AE⊥CD于E.
解:如图,作AE⊥CD于E.
四边形ABCD的面积=△ADE的面积+梯形ABCE的面积
=$\frac{1}{2}$×3×1+$\frac{1}{2}$×(2+3)×2
=1.5+5
=6.5;
∵AB=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,BC=2,CD=3,AD=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴四边形ABCD的周长=$\sqrt{5}$+2+3+$\sqrt{10}$=$\sqrt{5}$+5+$\sqrt{10}$.
点评 本题考查了勾股定理的应用,梯形的面积,三角形的面积,四边形的周长,熟练掌握勾股定理和面积公式是解决本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
3.如果二次函数y=x2-8x+c与x轴上只有一个公共点,那么c的值等于( )
| A. | 4 | B. | 8 | C. | -4 | D. | 16 |
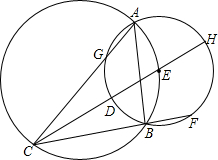 如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.
如图,⊙E的圆心在⊙O上,⊙E交⊙O于A、B两点,⊙O的弦CE所在直线交⊙E于点D、H,CB的延长线交⊙E于点F.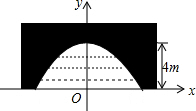 如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.
如图是一座古拱桥的截面图,拱桥洞是抛物线形状,其跨度为10m,桥洞与水面的最大距离为4m,将拱桥的横截面放在如图所示的平面直角坐标系中.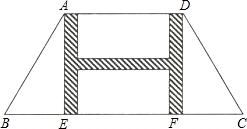 如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m.
如图,有一块等腰梯形的草坪,草坪上底AD长48m,下底BC长108m,上下底之间的距离AE(或DF)是40m.现要在草坪中修建横、纵向的“H”型甬道,甬道宽度相等,设甬道的宽为x m.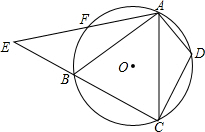 如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.
如图,△ABC内接于⊙O,D,F分别是$\widehat{AC}$与$\widehat{AB}$上的点,$\widehat{BF}$=$\widehat{DA}$,连接AF并延长交CB的延长线于点E,连接AD,CD,求证:△CDA∽△ABE.