题目内容
12.解方程(1)x2-5x-6=0
(2)3x2-4x-1=0;
(3)x(x-1)=3-3x;
(4)x2-2$\sqrt{2}$x+1=0.
分析 (1)根据因式分解法,可得方程的解;
(2)根据公式法,可得方程的解;
(3)根据因式分解法,可得方程的解;
(4)根据公式法,可得方程的解.
解答 解:(1)因式分解,得
(x-1)(x-6)=0,解得x1=6,x2=-1;
(2)a=3,b=-4,c=-1,x1=$\frac{2+\sqrt{7}}{3}$,x2=$\frac{2-\sqrt{7}}{3}$;
(3)方程化简得x2+2x-3=0,
因式分解,得(x+3)(x-1)=0,
解得x1=1,x2=-3;
(4)a=1,b=-2$\sqrt{2}$,c=1,x1=1+$\sqrt{2}$,x2=-1+$\sqrt{2}$.
点评 本题考查了解一元二次方程,根据方程的特点选择适当的方法是解题关键.

练习册系列答案
相关题目
20.点P(4,-2)所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.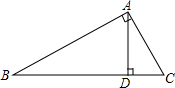 如图所示,下列说法不正确的是( )
如图所示,下列说法不正确的是( )
 如图所示,下列说法不正确的是( )
如图所示,下列说法不正确的是( )| A. | 点B到AC的垂线段是线段AB | B. | 点C到AB的垂线段是线段AC | ||
| C. | 线段AD是点D到AB的垂线段 | D. | 线段BD是点B到AD的垂线段 |