Question

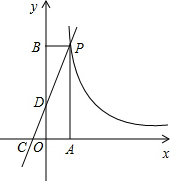如图，一次函数y=kx+2与反比例函数y=

m

x

x＞0）的图象相交于点P，PA⊥x轴于点A，PB⊥y轴于点B，一次函数的图象分别交x轴、y轴于点C、D，且S_△PBD=4，

OC

OA

=

1

2

．
（1）求点D的坐标及BD的长；
（2）求一次函数与反比例函数的解析式；
（3）N是反比例函数的图象上的一个动点，过点N作NM⊥x轴于点M，是否存在点N使得四边形DOMN的面积大于12且与以D、N、P、B为顶点的四边形的面积相等？若存在，求点N坐标；若不存在，请说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）根据y轴上点的横坐标等于0即可得出D点坐标，设点P（x，kx+2），可用x表示出A、B两点的坐标，根据

OC

OA

=

1

2

可得出C点坐标，进而可得出BD的长；
（2）根据S_△PBD=4，PB⊥y轴于点B可得出x的值，进而得出k的值，由此得出结论；
（3）设N（x，

12

x

），则S_{四边形DOMN}=

1

2

×（2+

12

x

）x=x+6，根据S_{四边形DOMN}＞12得出x的取值范围，故可得出点N在点P的右侧，连接BN，DN，则NM=

12

x

，OM=x，再由S_{四边形DOMN}=S_{四边形DNPB}，求出x的值，进而可得出结论．

解答：解：（1）∵D为直线y=kx+2与y轴的交点，
∴当x=0时，y=2，
∴D（0，2）．
∵P在y=kx+2图象上，设点P（x，kx+2），PB⊥y轴于点B，PA⊥x轴于点A，
∴B（0，kx+2），A（x，0）
∴BD=kx+2-2=kx，OA=x
∵

OC

OA

=

1

2

，OC=

1

2

x点C在x轴的负半轴，
∴C（-

1

2

x，0）
∵点C在y=kx+2上，
∴k（-

1

2

x）+2=0，即kx=4，
∴BD=4；

（2）∵S_△PBD=4，PB⊥y轴于点B，
∴

1

2

BD•BP=4，
∴

1

2

×4x=4，解得x=2，
∴k=2，P（2，6）
∴y=2x+2，y=

12

x

；

（3）设N（x，

12

x

），则S_{四边形DOMN}=

1

2

×（2+

12

x

）x=x+6，
∵S_{四边形DOMN}＞12，得x＞6，
∴点N在点P的右侧，
连接BN，DN，则NM=

12

x

，OM=x，
∵S_{四边形DOMN}=S_{四边形DNPB}，
∴

1

2

×2×（6-

12

x

）+

1

2

×4x=x+6，解得x²=12，
∴x=2

3

＜6，
∴满足条件的点N不存在．

点评：本题考查的是反比例函数综合题，涉及到一次函数及反比例函数图象上点的坐标特点等知识，难度适中．