题目内容
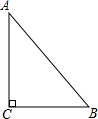 在Rt△ABC中∠C=90°,AB=6,sinA=
在Rt△ABC中∠C=90°,AB=6,sinA=| 2 |
| 3 |
| A、4 | ||||
B、2
| ||||
C、
| ||||
D、
|
考点:锐角三角函数的定义
专题:
分析:首先利用锐角三角函数关系得出BC的长,进而利用勾股定理得出AC的长.
解答:
解:∵在Rt△ABC中∠C=90°,AB=6,sinA=
,
∴
=
,即
=
,
解得:BC=4,
则AC的长为:
=
=2
.
故选:B.
| 2 |
| 3 |
∴
| BC |
| AB |
| 2 |
| 3 |
| BC |
| 6 |
| 2 |
| 3 |
解得:BC=4,
则AC的长为:
| AB2-BC2 |
| 62-42 |
| 5 |
故选:B.
点评:此题主要考查了锐角三角函数的定义以及勾股定理,利用锐角三角函数关系得出BC的长是解题关键.

练习册系列答案
相关题目
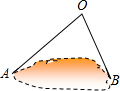 如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )
如图,为估计池塘岸边A、B两点的距离,小方在池塘的一侧选取一点O,测得OA=15米,OB=10米,A、B间的距离不可能是( )| A、5米 | B、10米 |
| C、15米 | D、20米 |
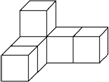 由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )
由6个大小相同的正方体搭成的几何体如图所示,关于它的视图,说法正确的是( )| A、主视图的面积最大 |
| B、左视图的面积最大 |
| C、俯视图的面积最大 |
| D、三个视图的面积一样大 |
已知代数式-
xa-1y3和3x-by2a+b是同类项,则a+3b的值为( )
| 1 |
| 2 |
| A、1 | B、-1 | C、3 | D、-3 |
 如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°. 如图,AB是⊙O的直径,C、D两点在⊙O上,若∠BAC为28°,则∠ADC=
如图,AB是⊙O的直径,C、D两点在⊙O上,若∠BAC为28°,则∠ADC= 如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=
如图,锐角△ABC内接于⊙O,作BD⊥AC于点D.过圆心O作OM⊥AB于点M,已知cosC=