题目内容
 如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.
如图所示,在△ABC中,AC=BC=4,∠C=90°,O是AB的中点,⊙O与AC、BC分别相切于点D、E,⊙O与AB相交于点F,连接DF并延长交CB的延长线于点G.(1)求证:∠BFG=∠BGF;
(2)求由DG、GE和弧ED所围成图形的面积.(阴影部分)
考点:切线的性质,扇形面积的计算
专题:
分析:(1)连接OD.根据切线的性质得到OD⊥AC,则OD∥BC;可得∠ODF=∠G,再结合对顶角相等和等边对等角得到∠BFG=∠BGF.
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
(2)阴影部分的面积=直角三角形CDG的面积-(正方形的面积-扇形ODE的面积).根据等腰直角三角形的性质可求出有关边AB、OD的长,以及圆心角∠DOE的度数.进而可根据扇形的面积和直角三角形的面积求得阴影部分的面积.
解答:解:(1)∵OD=OF(⊙O的半径),
∴∠ODF=∠OFD;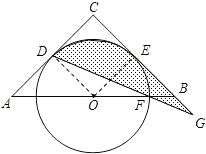
∵⊙O与AC相切于点D,
∴OD⊥AC;
又∵∠C=90°,即GC⊥AC,
∴OD∥GC,
∴∠BGF=∠ODF;
又∵∠BFG=∠OFD,
∴∠BFG=∠BGF.
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
AB=
=2
,
∴OD=
BC=
×4=2,
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=2
-2;
从而CG=CB+BG=2
+2;
∴S阴影=S△DCG-(S正方形ODCE-S扇形ODE)
=
×2×(2+2
)-(22-
π×22)
=π-2+2
.
∴∠ODF=∠OFD;

∵⊙O与AC相切于点D,
∴OD⊥AC;
又∵∠C=90°,即GC⊥AC,
∴OD∥GC,
∴∠BGF=∠ODF;
又∵∠BFG=∠OFD,
∴∠BFG=∠BGF.
(2)连OE,
∵⊙O与AC相切于点D、与BC相切于点E,
∴DC=CE,OD⊥AC,OE⊥BC,
∵∠C=90°,
∴四边形ODCE为正方形,
∵AO=BO=
| 1 |
| 2 |
| 1 |
| 2 |
| AC2+BC2 |
| 2 |
∴OD=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BFG=∠BGF,
∴BG=BF=OB-OF=2
| 2 |
从而CG=CB+BG=2
| 2 |
∴S阴影=S△DCG-(S正方形ODCE-S扇形ODE)
=
| 1 |
| 2 |
| 2 |
| 1 |
| 4 |
=π-2+2
| 2 |
点评:此题综合考查了切线的性质、平行线的性质、等腰直角三角形的性质及扇形的面积计算方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
轮船航行到C处观测小岛A的方向是北偏西48°,那么从A同时观测轮船的方向是( )
| A、南偏东42° |
| B、东偏北48° |
| C、南偏东48° |
| D、东偏南48° |
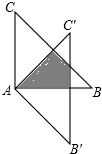 如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于
如图,△ABC绕点A顺时针旋转45°得到△A′B′C′,若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于
 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,先从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的共有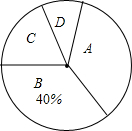 为了了解我校九年级男生立定跳远的成绩,从全校随机抽50名男生的测试成绩进行调查.根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成统计表和扇形图,如图:
为了了解我校九年级男生立定跳远的成绩,从全校随机抽50名男生的测试成绩进行调查.根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成统计表和扇形图,如图: 已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=
已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=3,DC=4,反比例函数y=