题目内容
6.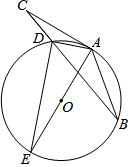 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.(1)求证:AB=AC;
(2)若sinE=$\frac{1}{3}$,AC=4$\sqrt{2}$,求△ADE的周长.
分析 (1)要证明AB=AC,只要证明∠C=∠B即可,根据题意可以求得∠C=∠B,从而可以证明结论成立;
(2)根据锐角三角函数和sinE=$\frac{1}{3}$,AC=4$\sqrt{2}$,可以分别求出AD、DE、EA的长,从而可以求得△ADE的周长.
解答  (1)证明:∵AD=DC,
(1)证明:∵AD=DC,
∴∠CAD=∠C,
∵AC是⊙O的切线,
∴∠CAE=90°,
∴∠CAD+∠EAD=90°,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴∠E+∠EAD=90°,
∴∠CAD=∠E,
又∵∠E=∠B,
∴∠C=∠B,
∴AB=AC;
(2)解:过点D作DF⊥AC于点F
∵DA=DC,AC=$4\sqrt{2}$,
∴CF=$\frac{1}{2}AC$=$2\sqrt{2}$,
∵∠C=∠E,sinE=$\frac{1}{3}$,
∴sinC=$\frac{1}{3}$,
∴sinC=$\frac{DF}{CD}$=$\frac{1}{3}$,
设DF=a,则CD=3a,
∵CF=2$\sqrt{2}$,
∴${a}^{2}+(2\sqrt{2})^{2}=(3a)^{2}$,
解得,a=1或a=-1(舍去),
∴DF=1,CD=3,
∴CD=DA=3,
∵在 Rt△ADE中,sinE=$\frac{1}{3}$,DA=3,
∴AE=9,ED=6$\sqrt{2}$,
∴△ADE的周长为:3+9+6$\sqrt{2}$=12+6$\sqrt{2}$.
点评 本题考查切线的性质、解直角三角形,解答本题的关键是明确题意,找出所求问题需要的条件,利用解直角三角形的相关知识解答.

练习册系列答案
相关题目
1.下列因式分解正确的是( )
| A. | x2-y2=(x-y)2 | B. | a2+a+1=(a+1)2 | ||
| C. | 2xy-6x=2x(y-3) | D. | a2+4a+21=a(a+4)+21 |
11.今年某县有1万名初中和小学生参加全国义务教育质量抽测,为了了解1万名学生的抽测成绩,从中抽取500名学生抽测成绩进行统计分析,在这个问题中数据500是( )
| A. | 总体 | B. | 个体 | C. | 一个样本 | D. | 样本容量 |
16.在-3,1,π,0.35 中,无理数是( )
| A. | -3 | B. | $\frac{1}{2}$ | C. | π | D. | 0.35 |