Question

1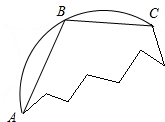．如图是一块残缺的圆轮片，点A、B、C在圆弧E上．
（1）画出$\widehat{AC}$所在的⊙O；
（2）若AB=BC=60，∠ABC=120°，求$\widehat{AC}$所在⊙O的半径．

Answer 1

分析 （1）利用垂径定理作出AB，BC的垂直平分线，交点即是圆心，到任意一点距离即是半径；
（2）利用垂径定理以及等边三角形的判定得出△OBC是等边三角形，即可得出答案．

解答 解（1）如图所示：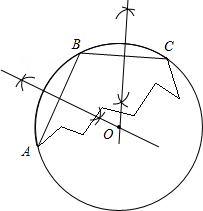

（2）如图，连接OA、OB、OC，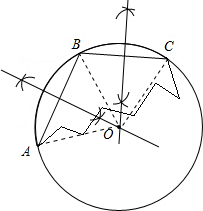

∵AB=BC=60，∠ABC=120°，
∴∠CBO=∠ABO=60°，
∵BO=CO，
∴∠OBC=∠BCO=60°，
∴△OBC是等边三角形，
∴半径为60．

点评 此题主要考查了垂径定理的应用，利用垂径定理得出∠CBO=∠ABO=60°，进而得出△OBC是等边三角形是解题关键．