题目内容
m为何整数时，关于x的方程3x2+6x+m=0有两个负实根？
解：设方程3x2+6x+m=0的两个负实根分别为x1、x2，
则有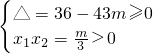
，即
；
∴0＜m≤3；
∴m=1，2，3．
分析：若方程有两个负实根，可得到两个条件：①方程的△＞0，②两根的积大于0；可列不等式组求出m的取值范围，进而可求出m的整数值．
点评：此题主要考查的是一元二次方程根与系数的关系及根的判别式．
则有
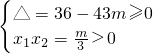，即；∴0＜m≤3；
∴m=1，2，3．
分析：若方程有两个负实根，可得到两个条件：①方程的△＞0，②两根的积大于0；可列不等式组求出m的取值范围，进而可求出m的整数值．
点评：此题主要考查的是一元二次方程根与系数的关系及根的判别式．
练习册系列答案
轻松暑假总复习系列答案
相关题目