题目内容
4．
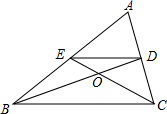如图所示，DE是△ABC的中位线，BD与CE相交于点O，则$\frac{OB}{OD}$的值是2．
分析 根据DE是△ABC的中位线可得出DE∥BC，DE=$\frac{1}{2}$BC，根据相似三角形的判定定理得出△ODE∽△OBC，由相似三角形的对应边成比例即可得出结论．
解答 解：∵DE是△ABC的中位线，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∴∠ODE=∠OBC，∠OED=∠OCB，
∴△ODE∽△OBC，
∴$\frac{OB}{OD}$=$\frac{BC}{DE}$=2．
故答案为：2．
点评 本题考查的是三角形中位线定理，熟知 三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
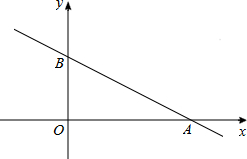如图，在以点O为原点的直角坐标系中，一次函数y=-$\frac{1}{2}$x+1的图象与x轴交于A，与y轴交于点B，求：
如图，在四边形ABCD中，∠A=90°，AB=3$\sqrt{3}$，AD=3，点M，N分别在边AB，BC上，点E，F分别为MN，DN的中点，连接EF，则EF长度的最大值为3．
12．已知一组数据：-2，5，2，-1，0，4，则这组数据的中位数是（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{4}{3}$ | D． | 2 |