题目内容
1.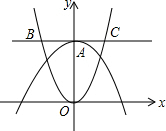 如图,抛物线y=ax2+1与y轴交于点A,过点A与x轴平行的直线交抛物线y=4x2于点B、C,则线段BC的长为1.
如图,抛物线y=ax2+1与y轴交于点A,过点A与x轴平行的直线交抛物线y=4x2于点B、C,则线段BC的长为1.
分析 先由y轴上点的横坐标为0求出A点坐标为(0,1),再将y=1代入y=4x2,求出x的值,得出B、C两点的坐标,进而求出BC的长度.
解答 解:∵抛物线y=ax2+1与y轴交于点A,
∴A点坐标为(0,1).
当y=1时,4x2=1,
解得x=±$\frac{1}{2}$,
∴B点坐标为(-$\frac{1}{2}$,1),C点坐标为($\frac{1}{2}$,1),
∴BC=$\frac{1}{2}$-(-$\frac{1}{2}$)=1,
故答案为:1.
点评 本题考查了二次函数的性质,两函数交点坐标的求法以及平行于x轴上的两点之间的距离的知识,解答本题的关键是求出点A的坐标,此题难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.商品原价389元,经连续两次降价后售价为279元,设平均每降价的百分率为x,则下面所列方程正确的是( )
| A. | 389(1-x)2=279 | B. | 279(1-x)2=389 | C. | 389(1-2x)=279 | D. | 279(1-2x)=389 |
9.符合下列条件的四边形不一定是菱形的是( )
| A. | 四边都相等 | B. | 两组邻边分别相等 | ||
| C. | 对角线互相垂直平分 | D. | 两条对角线分别平分一组对角 |
16. 如图,AB为⊙O的直径,点D、C在⊙O上,∠D=62°,则∠ACO的度数为( )
如图,AB为⊙O的直径,点D、C在⊙O上,∠D=62°,则∠ACO的度数为( )
 如图,AB为⊙O的直径,点D、C在⊙O上,∠D=62°,则∠ACO的度数为( )
如图,AB为⊙O的直径,点D、C在⊙O上,∠D=62°,则∠ACO的度数为( )| A. | 26° | B. | 28° | C. | 30° | D. | 32° |
 如图,求∠FAC+∠B+∠C+∠BDE+∠E+∠F的度数.
如图,求∠FAC+∠B+∠C+∠BDE+∠E+∠F的度数.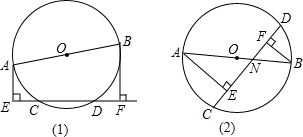
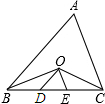 已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.
已知,如图,O是△ABC的∠ABC、∠ACB的角平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E,若BC=8cm,则△ODE的周长为8cm.