题目内容
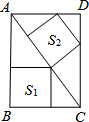 如图,在矩形ABCD中有2个正方形,如果它们的面积分别是S1、S2,AB=8cm,BC=6cm,那么S1、S2的大小关系是
如图,在矩形ABCD中有2个正方形,如果它们的面积分别是S1、S2,AB=8cm,BC=6cm,那么S1、S2的大小关系是考点:相似三角形的判定与性质
专题:
分析:作DE⊥AC于E,由勾股定理就可以得出AC,由三角形的面积公式就可以得出DE的值,设S1的正方形的边长为a,S2的正方形的边长为b,由正方形的性质及相似三角形的性质就可以求出a、b的值就可以结论.
解答:解:作DE⊥AC于E.
∵四边形ABCD是矩形,
∴∠D=∠B=90°,
在Rt△ADC中,由勾股定理,得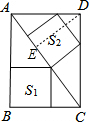
AC=
=10.
∴
=
,
∴DE=4.8.
设S1的正方形的边长为a,S2的正方形的边长为b,由题意,得
=
,
=
,
解得:a=
,b=
,
∵
>
,
∴S1>S2.
故答案为:S1>S2.
∵四边形ABCD是矩形,
∴∠D=∠B=90°,
在Rt△ADC中,由勾股定理,得

AC=
| 36+64 |
∴
| 6×8 |
| 2 |
| 10DE |
| 2 |
∴DE=4.8.
设S1的正方形的边长为a,S2的正方形的边长为b,由题意,得
| a |
| 6 |
| 8-a |
| 8 |
| b |
| 10 |
| 4.8-b |
| 4.8 |
解得:a=
| 24 |
| 7 |
| 120 |
| 37 |
∵
| 24 |
| 7 |
| 120 |
| 37 |
∴S1>S2.
故答案为:S1>S2.
点评:本题考查了矩形的性质的运用,正方形的性质的运用,相似三角形的性质的运用,三角形的面积公式的运用,解答时运用相似三角形的性质求解是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是一数值转换机,若输入的数为-
如图是一数值转换机,若输入的数为-| 1 |
| 2 |
| A、-6 | B、-3 | C、0 | D、3 |
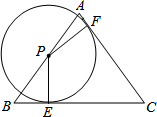 如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )A、
| ||
| B、2 | ||
C、
| ||
D、
|
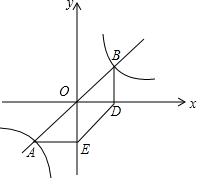 过原点的直线交反比例函数y=
过原点的直线交反比例函数y= 如图,线段AB和线段CD的重合部分CB的长度是线段AB长的
如图,线段AB和线段CD的重合部分CB的长度是线段AB长的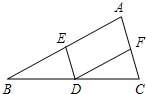 如图,在△ABC中,D点在BC边上,DE∥A C,DF∥AB.
如图,在△ABC中,D点在BC边上,DE∥A C,DF∥AB.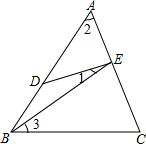 如图,
如图, 如图,在△ABC中,D是AB上一点,且∠ABC=∠ACD.
如图,在△ABC中,D是AB上一点,且∠ABC=∠ACD.