题目内容
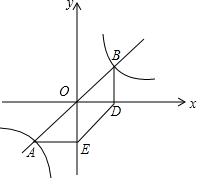 过原点的直线交反比例函数y=
过原点的直线交反比例函数y=| 12 |
| x |
(1)直线AB与直线ED的位置关系是什么?并说明理由.
(2)四边形ABDE的面积等于多少?
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据题意得出A、B关于原点对称,得出AE=OD,AE∥OD,从而证得四边形OAED是平行四边形,即可证得AB∥ED.
(2)根据反比例函数系数k的几何意义即可求得.
(2)根据反比例函数系数k的几何意义即可求得.
解答:解:(1)AB∥ED;理由如下:
∵过原点的直线交反比例函数y=
图象于A、B两点,
∴A、B关于原点对称,
∴AE=OD,
∵AE⊥y轴于点E.
∴AE∥x轴,
∴AE∥OD,
∴四边形OAED是平行四边形,
∴AB∥ED.
(2)∵四边形OAED是平行四边形,
∴S△AOE=S△EOD,
根据反比例函数系数k的几何意义:S△AOE=S△BOD=
×12=6,
∴四边形ABDE的面积=3×6=18.
∵过原点的直线交反比例函数y=
| 12 |
| x |
∴A、B关于原点对称,
∴AE=OD,
∵AE⊥y轴于点E.
∴AE∥x轴,
∴AE∥OD,
∴四边形OAED是平行四边形,
∴AB∥ED.
(2)∵四边形OAED是平行四边形,
∴S△AOE=S△EOD,
根据反比例函数系数k的几何意义:S△AOE=S△BOD=
| 1 |
| 2 |
∴四边形ABDE的面积=3×6=18.
点评:本题考查了反比例函数和一次函数的交点问题,平行四边形的判定和性质以及反比例函数系数k的几何意义.

练习册系列答案
相关题目
已知抛物线y=x2-x-1,与x轴的一个交点为(m,0),则代数式m2-m+2014的值为( )
| A、2013 | B、2015 |
| C、2014 | D、2010 |
 如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.
如图,∠CAB=90°,AD⊥BC,则∠CAD与∠B有何关系?并说明理由.
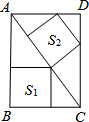 如图,在矩形ABCD中有2个正方形,如果它们的面积分别是S1、S2,AB=8cm,BC=6cm,那么S1、S2的大小关系是
如图,在矩形ABCD中有2个正方形,如果它们的面积分别是S1、S2,AB=8cm,BC=6cm,那么S1、S2的大小关系是 如图所示,两圆交于A、B两点,过B的直线交两圆于C、D,两圆外有一点P,连接PC,PD,分别交两圆于E,F.求证:P、E、A、F四点共圆.
如图所示,两圆交于A、B两点,过B的直线交两圆于C、D,两圆外有一点P,连接PC,PD,分别交两圆于E,F.求证:P、E、A、F四点共圆.