Question

四边形ABCD是正方形．

   (1)如图1－27(1)所示，点G是BC边上任意一点(不与B，C两点重合)，连接AG，作BF⊥AG于点F，DE⊥AG于点E．求证△ABF≌△DAE；

  (2)在(1)中，线段EF与AF，BF的等量关系是    ；(不需证明，直接写出结论即可)

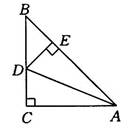
  (3)如图1－27(2)所示，若点G是CD边上任意一点(不与C，D两点重合)，作BF⊥AG于点F，DE⊥AG于点E，那么图中的全等三角形是    ，线段EF与AF，BF的等量关系是    ．(不需证明，直接写出结论即可)

Answer 1

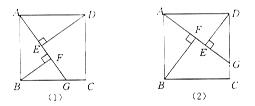
(1)证明：在正方形ABCD中，AB＝AD，∠BAD＝90°，∴∠BAF+∠DAE＝90°．在Rt△ABF中，∠BAF+∠ABF＝90°，∴∠ABF＝∠DAE．在△ABF与△DAE中，∠ABF＝∠DAE，∠AFB＝∠DEA＝90°，AB＝DA，∴△ABF≌△DAE(AAS)．(2)EF＝AF－BF  (3)△ABF≌△DAE   EF＝BF－AF