题目内容
14.计算:(1)$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-a}{a+1}$;
(2)$\frac{{a}^{2}-4}{{a}^{2}+4a+4}$•$\frac{2a}{{a}^{2}-4a+4}$.
(3)$\frac{1-{x}^{2}}{{x}^{2}+4x+4}$÷(x-1)2•$\frac{{x}^{2}+3x+2}{x-1}$.
(4)($\frac{3x}{x-1}$-$\frac{x}{x+1}$)•$\frac{{x}^{2}-1}{2x}$.
分析 (1)原式利用除法法则变形,约分即可得到结果;
(2)原式约分即可得到结果;
(3)原式利用除法法则变形,约分即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,约分即可得到结果.
解答 解:(1)原式=$\frac{(a+1)(a-1)}{(a+1)^{2}}$•$\frac{a+1}{a(a-1)}$=$\frac{1}{a}$;
(2)原式=$\frac{(a+2)(a-2)}{(a+2)^{2}}$•$\frac{2a}{(a-2)^{2}}$=$\frac{2a}{{a}^{2}-4}$;
(3)原式=$\frac{-(x+1)(x-1)}{(x+2)^{2}}$•$\frac{1}{(x-1)^{2}}$•$\frac{(x+1)(x+2)}{x-1}$=-$\frac{(x+1)^{2}}{(x+2)(x-1)^{2}}$;
(4)原式=$\frac{3{x}^{2}+3x-{x}^{2}+x}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{2x}$=$\frac{2x(x+2)}{2x}$=x+2.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.已知R=$\frac{2008×2009}{2010×2011}$,S=$\frac{2008×2010}{2009×2011}$,T=$\frac{2008×2011}{2009×2010}$,则( )
| A. | R>S>T | B. | T>S>R | C. | S>T>R | D. | S>R>T |
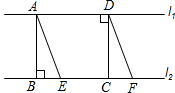 如图,直线l1∥l2,点A、D在l1上,AB⊥l1,CD⊥l2,垂足分别是B、C,点E,F在l2上,AE∥DF,那么AE与DF、BE与CF相等吗?为什么?
如图,直线l1∥l2,点A、D在l1上,AB⊥l1,CD⊥l2,垂足分别是B、C,点E,F在l2上,AE∥DF,那么AE与DF、BE与CF相等吗?为什么?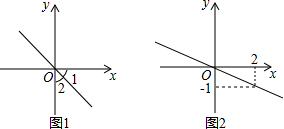 由正比例函数图象写出函数解析式
由正比例函数图象写出函数解析式 如图,A城气象台测得台风中心在A城正西方向300km处,以每小时10$\sqrt{7}$km的速度向北偏东60°的BF方向移动,距台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向300km处,以每小时10$\sqrt{7}$km的速度向北偏东60°的BF方向移动,距台风中心200km的范围内是受台风影响的区域.