Question

1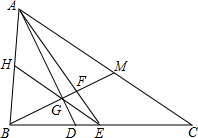．如图，在△ABC中，AC＞AB，AD是角平分线，AE是中线，BF⊥AD于点G，交AE于点F，交AC于点M，EG的延长线交AB于点H．
（1）求证：AH=BH；
（2）若∠BAC=60°，求$\frac{FG}{DG}$的值．

Answer 1

分析 （1）求出BG=MG，根据三角形的中位线性质求出GE∥AC，推出$\frac{BH}{AH}$=$\frac{BE}{CE}$，即可得出答案；
（2）延长EH到P，使GH=HP，连接AP和BP，求出四边形APBG是平行四边形，根据平行四边形的性质得出平行，得出比例式$\frac{GF}{BG}$=$\frac{GE}{PE}$，同理$\frac{GD}{AG}$=$\frac{GE}{PE}$，求出$\frac{GF}{GD}$=$\frac{BG}{AG}$，求出$\frac{BG}{AG}$=tan30°=$\frac{\sqrt{3}}{3}$，即可得出答案．

解答 （1）证明：∵BF⊥AD，
∴∠ABG+∠BAG=90°，∠AMG+∠MAG=90°，
∵AD是角平分线，
∴∠BAG=∠MAG，
∴∠ABG=∠AMG，
∴AB=AM，
∴BG=MG，
∵BE=EC，
∴GE∥AC，
∴$\frac{BH}{AH}$=$\frac{BE}{CE}$，
∴AH=BH；


（2）解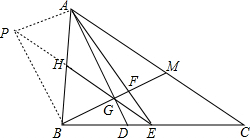：延长EH到P，使GH=HP，连接AP和BP，
∵AH=BH，
∴四边形APBG是平行四边形，
∴AP=BG，AP∥BG，
∴$\frac{GF}{PA}$=$\frac{GE}{PE}$，
∴$\frac{GF}{BG}$=$\frac{GE}{PE}$，
同理，$\frac{GD}{AG}$=$\frac{GE}{PE}$，
∴$\frac{GF}{BG}$=$\frac{GD}{AG}$，
∴$\frac{GF}{GD}$=$\frac{BG}{AG}$，
∵∠BAC=60°，AD是角平分线，
∴∠BAG=30°，
在Rt△ABG中，$\frac{BG}{AG}$=tan30°=$\frac{\sqrt{3}}{3}$，
∴$\frac{FG}{DG}$=$\frac{\sqrt{3}}{3}$．

点评 本题考查了平行四边形的性质和判定，解直角三角形，平行线分线段成比例定理的应用，能综合运用知识点进行推理和计算是解此题的关键．