题目内容
16.已知x=$\sqrt{6}$+$\sqrt{5}$,则(x+$\frac{1}{x}$):(x-$\frac{1}{x}$)等于$\frac{\sqrt{30}}{5}$.分析 根据x的值,求出$\frac{1}{x}$的值,代入代数式化简即可.
解答 解:由x=$\sqrt{6}$+$\sqrt{5}$,
得$\frac{1}{x}=\frac{1}{\sqrt{6}+\sqrt{5}}=\sqrt{6}-\sqrt{5}$,
∴(x+$\frac{1}{x}$):(x-$\frac{1}{x}$)
=$\frac{\sqrt{6}+\sqrt{5}+\sqrt{6}-\sqrt{5}}{\sqrt{6}+\sqrt{5}-\sqrt{6}+\sqrt{5}}$
=$\frac{\sqrt{6}}{\sqrt{5}}$
=$\frac{\sqrt{30}}{5}$.
故答案为:$\frac{\sqrt{30}}{5}$.
点评 本题考查了二次根式的化简,特别是分式的分母有理化,是进行分式化简和变形的基础.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.观察下列图形:按照这样的规律,第n个图形有( )个★.


| A. | 3n-1 | B. | 3n+1 | C. | 3n+4 | D. | 4n+3 |
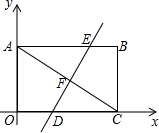 如图,平面直角坐标系中,把矩形OABC沿直线DE对折使点C落在点A(0,6)处,DE与AC相交于点F,且$\frac{EF}{AF}$=$\frac{\sqrt{3}}{3}$.
如图,平面直角坐标系中,把矩形OABC沿直线DE对折使点C落在点A(0,6)处,DE与AC相交于点F,且$\frac{EF}{AF}$=$\frac{\sqrt{3}}{3}$. 如图,已知在⊙O中M是弧AB的中点,N是弦AB的中点,AB=2$\sqrt{3}$,MN=1,求:圆心到AB的距离.
如图,已知在⊙O中M是弧AB的中点,N是弦AB的中点,AB=2$\sqrt{3}$,MN=1,求:圆心到AB的距离.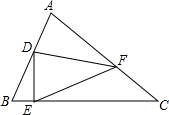 如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.
如图,在△ABC中,∠ACB=45°,D是AB边的中点,点E在BC边上,点F在AC边上,DE⊥DF,连接EF,若BE=1,EF=5,则线段AF的长为3$\sqrt{2}$.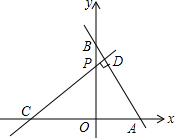 如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.
如图.在平面直角坐标系中,点C、点A为x轴上两点,OA、OC的长是方程y=x2-7x+12=0的两个根(OC>OA).点B在y轴上,CD⊥AB交y轴于点P,且CP=AB.