题目内容
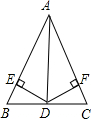 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,则下列说法:①DA平分∠EDF;②AE=AF,DE=DF;③AD上任意一点到B、C两点的距离相等;④图中共有3对全等三角形,其中正确的有考点:等腰三角形的性质,全等三角形的判定,角平分线的性质
专题:
分析:由等腰三角形的性质结合条件可证明△ADE≌△ADF,可判断①②正确,结合条件可知AD是BC的垂直平分线,可判定③正确,结合条件可证明△BDE≌△CDF,△ABD≌△ACD,可判断④正确.
解答:解:∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠DAE=∠DAF,∠DEA=∠DFA,
在△ADE和△ADF中,
,
∴△ADE≌△ADF(AAS),
∴AE=AF,DE=DF,∠ADE=∠ADF,
∴①②正确;
又∵AB=AC,AD是∠BAC的角平分线,
∴AD垂直平分线段BC,
∴③正确;
在△ABD和△ACD中,
,
∴△ABD≌△ACD(SAS),
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴全等的三角形共有三对,
∴④正确,
综上可知正确的为①②③④,
故答案为:①②③④.
∴∠DAE=∠DAF,∠DEA=∠DFA,
在△ADE和△ADF中,
|
∴△ADE≌△ADF(AAS),
∴AE=AF,DE=DF,∠ADE=∠ADF,
∴①②正确;
又∵AB=AC,AD是∠BAC的角平分线,
∴AD垂直平分线段BC,
∴③正确;
在△ABD和△ACD中,
|
∴△ABD≌△ACD(SAS),
在Rt△BDE和Rt△CDF中,
|
∴Rt△BDE≌Rt△CDF(HL),
∴全等的三角形共有三对,
∴④正确,
综上可知正确的为①②③④,
故答案为:①②③④.
点评:本题主要考查等腰三角形的性质和全等三角形的判定,掌握全等三角形底边上的中线、底边上的高和顶角的角平分线相互重合是解题的关键.

练习册系列答案
相关题目
在-2,3,
,0,-5,+11,-
,-9,0.02中,负整数共有( )
| 5 |
| 3 |
| 3 |
| 7 |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列积为正值的是( )
| A、(-2)×3×4×(-1) |
| B、(-5)×(-6)×3×(-2) |
| C、(-2)×(-2)×(-2) |
| D、(-3)×(-3)×(-3)×0 |
下列四个点中,在反比例函数y=
的图象上的是( )
| -6 |
| x |
| A、(-3,-2) |
| B、(3,2) |
| C、(-2,3) |
| D、(-2,-3) |