题目内容
2.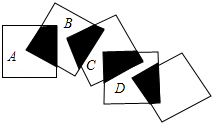 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
分析 如图AB、AF.由△ABE≌△AFG,推出S△ABE=S△AFG,推出S四边形AEBG=S△ABF=$\frac{1}{4}$S正方形,推出S阴=4×$\frac{1}{4}$S正方形=9即可解决问题.
解答 解:如图AB、AF.
∵∠EAG=∠BAF=90°,
∴∠BAE=∠FAG,
在△ABE和△AFG中,
$\left\{\begin{array}{l}{∠ABE=∠AFG=45°}\\{AB=AF}\\{∠BAE=∠FAG}\end{array}\right.$,
∴△ABE≌△AFG,
∴S△ABE=S△AFG,
∴S四边形AEBG=S△ABF=$\frac{1}{4}$S正方形,
∴S阴=4×$\frac{1}{4}$S正方形=9,
故选C.
点评 本题考查正方形的性质、全等三角形的判定和性质等知识,证明每一个阴影部分的面积等于正方形的面积的$\frac{1}{4}$是解题的关键.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | (ab)2=ab2 | B. | 5a2-3a2=2 | C. | a(b+2)=ab+2 | D. | 5a3•3a2=15a5 |
13.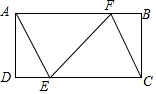 如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )
如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )
 如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )
如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )| A. | 5 | B. | $\frac{15}{4}$ | C. | $\sqrt{10}$ | D. | $\sqrt{26}$ |
10.下列四边形中,是轴对称图形但不是中心对称图形的是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 菱形 | D. | 矩形 |
17.三元一次方程组$\left\{\begin{array}{l}x-y=1\\ y-z=1\\ x+z=6\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=2\\ y=3\\ z=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=2\\ y=4\\ z=3\end{array}\right.$ | C. | $\left\{\begin{array}{l}x=3\\ y=2\\ z=4\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=4\\ y=3\\ z=2\end{array}\right.$ |
7.直线y=-x-2与两坐标轴围成的图形的面积是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
14.下列各数:$\frac{23}{7}$、1.414、0.$\stackrel{••}{72}$、$\root{3}{-8}$、$\root{3}{16}$中,其中无理数有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.据初步统计,2017年春节期间,安徽省累计接待游客2681.52万人次,实现旅游总收入142亿元,其中142亿用科学记数法表示为( )
| A. | 1.42×108 | B. | 1.42×109 | C. | 1.42×1010 | D. | 1.42×1011 |
12.已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(2,4),则它们的另一个交点坐标是( )
| A. | (-2,4) | B. | (-4,-2) | C. | (4,2) | D. | (-2,-4) |