题目内容
13.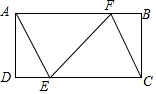 如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )
如图,矩形ABCD中,AD=3,AB=9,过点A,C作相距为3的平行线段AE,CF,分别交CD,AB于点E,F,则FE的长是( )| A. | 5 | B. | $\frac{15}{4}$ | C. | $\sqrt{10}$ | D. | $\sqrt{26}$ |
分析 过F作FH⊥AE于H,根据矩形的性质得到AB=CD,AB∥CD,推出四边形AECF是平行四边形,根据平行四边形的性质得到AF=CE,根据相似三角形的性质得到比例式,于是得到AE=AF,列方程即可得到DE的长,再由勾股定理求出AE=AF=5,得出HE的长,然后由勾股定理求出EF的长即可.
解答 解:过F作FH⊥AE于H,如图所示:
则FH=3=AD,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∵AE∥CF,
∴四边形AECF是平行四边形,
∴AF=CE,
∴DE=BF,
∴AF=9-DE,
∴AE=$\sqrt{9+D{E}^{2}}$,
∵∠FHA=∠D=∠DAF=90°,
∴∠AFH+∠HAF=∠DAE+∠FAH=90°,
∴∠DAE=∠AFH,
∴△ADE∽△AFH,
∴$\frac{AE}{AF}=\frac{AD}{FH}$=$\frac{DE}{AH}$=1,
∴AE=AF,DE=AH,
∴$\sqrt{9+D{E}^{2}}$=9-DE,
解得:DE=4,
∴AH=4,
∴AF=AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5,
∴HE=AE-AH=1,
∴EF=$\sqrt{H{E}^{2}+H{F}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$;
故选:C.
点评 本题考查了矩形的性质,相似三角形的判定和性质,勾股定理,平行四边形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键.

练习册系列答案
相关题目
3.化简:(1+$\frac{1}{x-2}$)÷$\frac{x-1}{{x}^{2}-2x}$结果为( )
| A. | 4x | B. | 3x | C. | 2x | D. | x |
4.-1$\frac{1}{2}$的倒数的绝对值是( )
| A. | $\frac{2}{3}$ | B. | -1$\frac{1}{2}$ | C. | 1$\frac{1}{2}$ | D. | $-\frac{2}{3}$ |
1.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
| A. | $\left\{{\begin{array}{l}{7y=x+3}\\{8y+5=x}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{7y=x-3}\\{8y+5=x}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{7y=x+3}\\{8y=x+5}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{7y=x-3}\\{8y=x+5}\end{array}}\right.$ |
8.关于x的一元二次方程(k-1)x2-2x+3=0有两个不相等的实根,则k的取值范围是( )
| A. | k<$\frac{4}{3}$ | B. | k<$\frac{4}{3}$且k≠1 | C. | 0≤k≤$\frac{4}{3}$ | D. | k≠1 |
5.在下列各数中,是无理数的是( )
| A. | $\frac{15}{7}$ | B. | π | C. | $\sqrt{49}$ | D. | $\root{5}{32}$ |
2.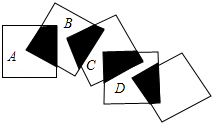 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
3.把n边形变为(n+x)边形,内角和增加了720°,则x的值为( )
| A. | 4 | B. | 6 | C. | 5 | D. | 3 |