题目内容
7.直线y=-x-2与两坐标轴围成的图形的面积是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
分析 将一次函数与x轴,y轴的交点坐标求出即可求出该直线与坐标轴围成三角形的面积.
解答 解:令x=0代入y=-x-2,
∴y=-2,
令y=0代入y=-x-2,
∴x=2,
∴直线y=-x-2与两坐标轴围成的图形的面积是:$\frac{1}{2}$×2×2=2,
故选(C)
点评 本题考查一次函数图象上点的特征,解题的关键是求出一次函数与坐标轴的交点坐标,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列各实数中,最大的是( )
| A. | |-2| | B. | 20 | C. | 2-1 | D. | $\sqrt{2}$ |
2.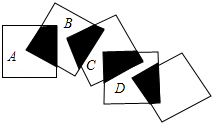 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
 将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
将五个边长都为3cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )| A. | 3cm2 | B. | 6cm2 | C. | 9cm2 | D. | 18cm2 |
12.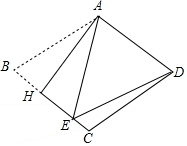 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
 如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )
如图,把菱形ABCD沿AH折叠,B落在BC边上的点E处.若∠BAE=40°,则∠EDC的大小为( )| A. | 10° | B. | 15° | C. | 18° | D. | 20° |
19.下列图形中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
16.3的绝对值是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
17.计算(-2)2002+(-2)2001所得的正确结果是( )
| A. | 22001 | B. | -22001 | C. | 1 | D. | 2 |