Question

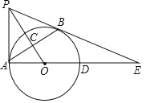
【题目】如图，PA与⊙O相切于点A，过点A作AB⊥OP，垂足为C，交⊙O于点B．连接PB，AO，并延长AO交⊙O于点D，与PB的延长线交于点E．

(1)求证：PB是⊙O的切线；

(2)若OC=3，AC=4，求PB的长．

Answer 1

【答案】（1）见解析；（2）PB＝

【解析】

（1）要证明是圆的切线，须证明过切点的半径垂直，所以连接OB，证明OB⊥PE即可．

（2）先证明△ACO∽△PAO，然后利用相似三角形的性质求出PO，再利用勾股定理求出PA，即可得到PB的长度.

（1）证明：连接OB，如图：

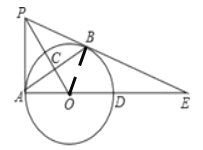
∵PA与⊙O相切于点A，

∴∠OAP＝90°

∵PO⊥AB，

∴AC＝BC，

∴PA＝PB，

在△PAO和△PBO中

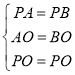
∴△PAO≌△PBO

∴∠OBP＝∠OAP＝90°

∴PB是⊙O的切线．

（2）在Rt△ACO中，OC＝3，AC＝4

∴AO＝5

在Rt△ACO与Rt△PAO中，

∵∠AOC＝∠POA，∠PAO＝∠ACO＝90°

∴△ACO∽△PAO

∴

∴PO＝，

由勾股定理，得：

，

∴PB＝PA＝.