题目内容
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

【答案】![]() 或
或![]() .
.
【解析】由图可知,在△OMN中,∠OMN的度数是一个定值,且∠OMN不为直角. 故当∠ONM=90°或∠MON=90°时,△OMN是直角三角形. 因此,本题需要按以下两种情况分别求解.
(1) 当∠ONM=90°时,则DN⊥BC.
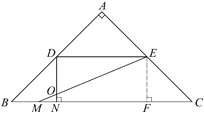
过点E作EF⊥BC,垂足为F.(如图)
∵在Rt△ABC中,∠A=90°,AB=AC,
∴∠C=45°,
∵BC=20,
∴在Rt△ABC中, ![]() ,
,
∵DE是△ABC的中位线,
∴![]() ,
,
∴在Rt△CFE中, ![]() ,
, ![]() .
.
∵BM=3,BC=20,FC=5,
∴MF=BC-BM-FC=20-3-5=12.
∵EF=5,MF=12,
∴在Rt△MFE中, ![]() ,
,
∵DE是△ABC的中位线,BC=20,
∴![]() ,DE∥BC,
,DE∥BC,
∴∠DEM=∠EMF,即∠DEO=∠EMF,
∴![]() ,
,
∴在Rt△ODE中, ![]() .
.
(2) 当∠MON=90°时,则DN⊥ME.
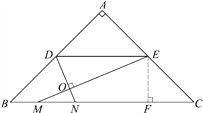
过点E作EF⊥BC,垂足为F.(如图)
∵EF=5,MF=12,
∴在Rt△MFE中, ![]() ,
,
∴在Rt△MFE中, ![]() ,
,
∵∠DEO=∠EMF,
∴![]() ,
,
∵DE=10,
∴在Rt△DOE中, ![]() .
.
综上所述,DO的长是![]() 或
或![]() .
.
故本题应填写: ![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目