题目内容
20.如图,草地边缘OM与小河河岸ON在点O处形成30°的夹角,牧马人从A地出发,先让马到草地吃草,然后再去河边饮水,最后回到A地.已知OA=2km,请在图中设计一条路线,使所走的路径最短,并求出整个过程所行的路程.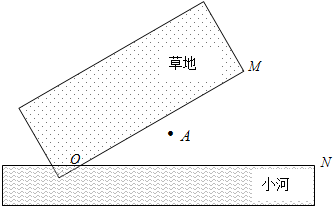
分析 分别画出点A关于OM、ON的对称点B、C,连接BC交OM、ON于点D、E,连接AD、AE,则线段AD、DE、EA即为所示路径,根据已知和等边三角形的性质得到答案.
解答 解:分别画出点A关于OM、ON的对称点B、C,连接BC交OM、ON于点D、E,连接AD、AE,则线段AD、DE、EA即为所示路径;
由题意得,OB=OA=2,
数据线OBC为等边三角形,
∴BC=2,故其总路程为2km.
点评 本题考查的是轴对称--最短路线问题,根据轴对称确定最短路线是解题的关键,注意等边三角形的性质的灵活运用.

练习册系列答案
相关题目
12.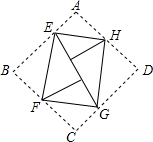 如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
 如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )
如图,有一个长(AB)为10cm的矩形纸板(即矩形ABCD),现将这个纸板的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH.若EF=8cm,则四边形EFGH的面积为( )| A. | 36cm2 | B. | 48cm2 | C. | 64cm2 | D. | 72cm2 |
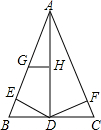 如图,已知AB=AC,AD是中线,BE=CF.
如图,已知AB=AC,AD是中线,BE=CF.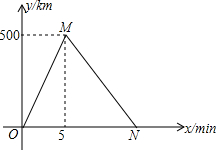 小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象.
小亮和小华的家住在滨河大道旁,周六早上,他们两个相约去滨河大道上训练跑步,他们从A路口出发,沿滨河大道跑到B路口再原路返回,因为体力的原因,他们返回的平均速度都是各自出发时速度的$\frac{4}{5}$,设出发时间为x min,距A路口的距离为y cm,图中折线表示小亮在整个训练过程中y与x之间的函数关系图象. 如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).
如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).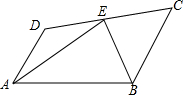 如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.
如图,E是线段CD上的一点,EA、EB分别平分∠DAB和∠CBA,∠AEB=90°,设AD=x,BC=y,且(x-3)2+|y-1|=0.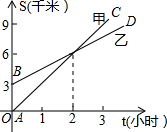 如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.
如图,已知A地在B地的正南方3千米处,甲、乙两人同时分别从A、B两地向正北方向匀速行驶,他们与A地的而距离(千米)与所行的时间(时)之间的函数关系如图中AC和BD所示,当他们行驶了4小时后,他们之间的距离为3千米.