题目内容
6.已知a1=x+1(x≠0且x≠-1),a2=1÷(1-a1),a3=1÷(1-a2),…,an=1÷(1-an-1),则a2016等于$\frac{x}{x+1}$.分析 题目属于规律型题目,首先根据已知条件,逐个求出,进而发现规律,每三个代数式一个循环,然后,利用除法算出2016÷3=672,可以求得题目答案.
解答 解:a1=x+1
a2=1÷(1-a1)=-$\frac{1}{x}$
a3=1÷(1-a2)=$\frac{x}{x+1}$
a4=1÷(1-a3)=x+1…
由此规律发现,每三个代数式一个循环,
∴2016÷3=672
∴a2016=a3=$\frac{x}{x+1}$
故答案:$\frac{x}{x+1}$
点评 做规律型题目要有耐心,首先算出每个代数式的值,进而发现规律,即可求出题目答案.题目设置巧妙,可以考查学生发现问题和处理问题的能力.

练习册系列答案
相关题目
16.在梯形ABCD中,AD∥BC,∠A:∠B:∠C:∠D可以是( )
| A. | 3:5:6:4 | B. | 3:4:5:6 | C. | 4:5:6:3 | D. | 6:5:4:3 |
18. 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
 如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )
如图,在4×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,则tan∠ACB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
15.A、B两地相距30千米,甲从A地出发以每小时5千米的速度向目的地B行走,则甲与B地间的距离s(千米)与甲行走的时间t(小时)间的函数关系是( )
| A. | s=5t(t≥0) | B. | s=5t(0≤t≤6) | C. | s=30+5t(0≤t≤6) | D. | s=30-5t(0≤t≤6) |
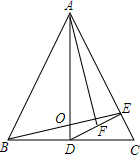 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,DE⊥AC,垂足为E,且DF=EF,求证:AF⊥BE.