题目内容
10. 如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.
如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.
分析 由B、C的坐标为(-10,0)、(-10,5),可求得OB与BC的长,然后分别从△OPQ≌△BCO,△OPQ≌△BOC去分析求解即可求得答案.
解答 解:∵B、C的坐标为(-10,0)、(-10,5),
∴OB=10,BC=5,∠OBC=90°.
∵PO⊥OQ,
∴∠POQ=90°.
△OBC和以P、Q、O为顶点的三角形全等时,分两种情况:
①如果△OPQ≌△BCO,
那么OP=BC=5,OQ=BO=10,
∵P、Q两点分别是x轴、y轴上的动点,
∴P(±5,0),Q(0,±10);
②如果△OPQ≌△BOC,
那么OP=BO=10,OQ=BC=5,
∵P、Q两点分别是x轴、y轴上的动点,
∴P(±10,0),Q(0,±5).
故P(±5,0),Q(0,±10)或P(±10,0),Q(0,±5).
点评 此题考查了全等三角形的判定与性质以及坐标与图形性质.此题难度适中,注意掌握分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
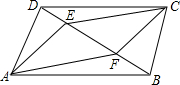 如图,已知AB∥DC,且AB=CD,BF=DE,试说明AF∥CE.
如图,已知AB∥DC,且AB=CD,BF=DE,试说明AF∥CE.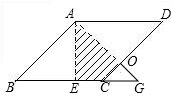 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?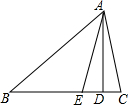 如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.
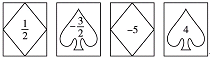
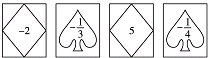
如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC. 的卡片,那么加上卡片上的数字,如果抽到形如
的卡片,那么加上卡片上的数字,如果抽到形如 的卡片,那么减去卡片上的数字;
的卡片,那么减去卡片上的数字;