题目内容
2. 如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.
如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.
分析 设AC=x,BC=4-x,根据等腰直角三角形性质,得出CD=$\frac{\sqrt{2}}{2}$x,CD′=$\frac{\sqrt{2}}{2}$(4-x),根据勾股定理然后用配方法即可求解.
解答 解:设AC=x,BC=4-x,
∵△ABC,△BCD′均为等腰直角三角形,
∴CD=$\frac{\sqrt{2}}{2}$x,CD′=$\frac{\sqrt{2}}{2}$(4-x),
∵∠ACD=45°,∠BCD′=45°,
∴∠DCE=90°,
∴DE2=CD2+CE2=$\frac{1}{2}$x2+$\frac{1}{2}$(4-x)2=x2-4x+8=(x-2)2+4,
∵根据二次函数的最值,
∴当x取2时,DE取最小值,最小值为:2.
故答案为:2.
点评 本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.正方形一边上任意一点到这个正方形两条对角线的距离之和等于对角线的( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2倍 |
7.两直线相交形成的4个角的度数之比依次可能是( )
| A. | 2:3:2:3 | B. | 1:1:4:4 | C. | 1:2:3:4 | D. | 3:4:4:3 |
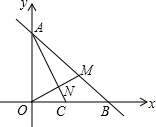 如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4.
如图,直线y=-x+m与x轴交于点B(4,0),与y轴交于点A,点C为OB上一点,点M为AB上一点,OM交AC于N,S△ABC=4.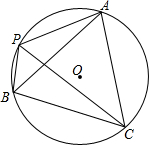 如图:已知AB=AC,∠APC=60°.
如图:已知AB=AC,∠APC=60°.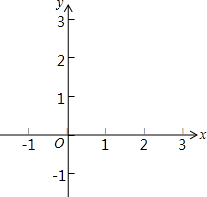 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.