题目内容
2.正方形一边上任意一点到这个正方形两条对角线的距离之和等于对角线的( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 2倍 |
分析 作PM⊥AC于M,PN⊥BD于N;由正方形的性质得出△AMP是等腰直角三角形,四边形OMPN是矩形,得出PM=AM,PN=OM,即可得出结论.
解答 解:如图所示: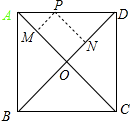 作PM⊥AC于M,PN⊥BD于N;
作PM⊥AC于M,PN⊥BD于N;
则∠PMA=∠OMP=∠ONP=90°,
∵四边形ABCD是正方形,
∴∠PAM=45°,OA=$\frac{1}{2}$AC,AC=BD,AC⊥BD,
∴△AMP是等腰直角三角形,四边形OMPN是矩形,
∴PM=AM,PN=OM,
∴PM+PN=AM+OM=OA=$\frac{1}{2}$AC;
故选:B.
点评 本题考查了正方形的性质、等腰直角三角形的判定与性质、矩形的判定与性质;熟练掌握正方形的性质,通过作辅助线得出等腰直角三角形和矩形是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
10.下列运算正确的是( )
| A. | (-2a2)3=8a6 | B. | (3a+b)2=9a2+b2 | C. | a2•a3=a5 | D. | a2+a3=a5 |
14.矩形具有而菱形不具有的性质是( )
| A. | 对角线相等 | B. | 对角线平分一组对角 | ||
| C. | 对角线互相平分 | D. | 对角线互相垂直 |
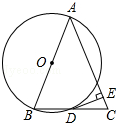 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作DE⊥AC于点E
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点恰好为BC的中点D,过点D作DE⊥AC于点E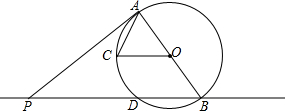
 如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.
如图,线段AB的长为4,C为AB上一动点,分别以AC、BC为斜边在AB的同侧作等腰直角△ACD和等腰直角△BCE,那么DE长的最小值是2.