Question

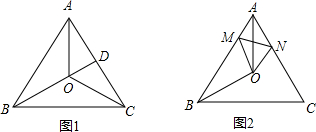
点A、B、C是平面内不在同一条直线上的三点，点D是此平面内任意一点，若A、B、C、D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有

 

个．

Answer 1

考点：平行四边形的判定

专题：

分析：分别过A、B、C三点作直线l∥BC、m∥AC、n∥AB，分别交于点D、E、F，根据平行四边形的判定方法可知D、E、F为满足条件的点．

解答：解：如图，连接AB、BC、CA，分别过A、B、C三点作直线l∥BC、m∥AC、n∥AB，分别交于点D、E、F，

∵AF∥BC，AB∥CF，
∴四边形ABCF为平行四边形，
同理可知四边形ABEC、四边形ADBC也为平行四边形，
故D、E、F三点为满足条件的D点，
故答案为：3．

点评：本题主要考查平行四边形的判定方法，掌握平行四边形的判定方法是解题的关键，即①两组对边分别平行，②两组对边分别相等，③一组对边平行且相等，④两组对角分别相等，⑤对角线互相平分的四边形是平行四边形．