题目内容
1.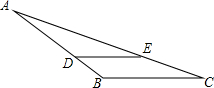 如图,△ABC∽△ADE,AD=8cm,BD=4cm,BC=15cm,EC=7cm.
如图,△ABC∽△ADE,AD=8cm,BD=4cm,BC=15cm,EC=7cm.(1)DE∥BC吗?为什么?
(2)求DE,AE的长.
(3)你还能发现哪些线段成比例?
分析 (1)根据相似三角形的对应角相等得到∠B=∠ADE,然后根据平行线的判定得DE∥BC;
(2)根据相似三角形的对应边的比相等得到即$\frac{DE}{15}$=$\frac{AE}{AE+7}$=$\frac{8}{8+4}$,然后利用比例性质求DE和AE的长;
(3)由计算的结果易得$\frac{AD}{DB}$=$\frac{AE}{EC}$.
解答 解:(1)DE∥BC.理由如下:
∵△ABC∽△ADE,
∴∠B=∠ADE,
∴DE∥BC;
(2)∵△ABC∽△ADE,
∴$\frac{DE}{BC}$=$\frac{AE}{AC}$=$\frac{AD}{AB}$,即$\frac{DE}{15}$=$\frac{AE}{AE+7}$=$\frac{8}{8+4}$,
∴DE=10cm,AE=14cm;
(3)成比例线段还有:$\frac{AD}{DB}$=$\frac{AE}{EC}$.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等.相似三角形(多边形)的周长的比等于相似比.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
6.如果a的相反数是1,那么a等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 无法确定 |
11.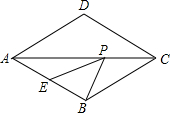 如图,在菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
 如图,在菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )
如图,在菱形ABCD中,AB=4,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值为( )| A. | 4 | B. | 5 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{5}$ |