题目内容
17. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )| A. | 135° | B. | 125° | C. | 90° | D. | 60° |
分析 连接OD,根据切线的性质可得△ODC是直角三角形,则∠DOC的度数即可求得,然后根据等腰三角形的外角的性质求得∠ADO的度数,则∠CDA即可求得.
解答  解:连接OD.
解:连接OD.
∵CD是圆的切线,
∴OD⊥CD,即∠ODC=90°,
∴∠DOC=90°-∠C=90°-20°=70°,
∵OD=OA,
∴∠ADO=∠A,
又∵∠DOC=∠ADO+∠A,
∴∠ADO=35°,
∴∠CDA=∠ODC+∠ADO=90°+35°=125°.
故选B.
点评 本题考查了切线的性质以及等腰三角形的性质,已知圆的切线常用的辅助线是连接圆心和切点.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
9.如果$\sqrt{(2a-1)^{2}}$=2a-1,那么a的取值范围( )
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
5.下列语句中,不正确的有( )
①直径是弦;
②弧是半圆;
③经过圆内一定点可以作无数条弦;
④长度相等的弧是等弧.
①直径是弦;
②弧是半圆;
③经过圆内一定点可以作无数条弦;
④长度相等的弧是等弧.
| A. | ①③④ | B. | ②③ | C. | ② | D. | ②④ |
5.(-$\frac{5}{13}$)2015×(-2$\frac{3}{5}$)2016的值是( )
| A. | -1 | B. | 1 | C. | -$\frac{13}{5}$ | D. | $\frac{5}{13}$ |
4.-( $\frac{1}{2}$-$\frac{1}{3}$)的相反数是( )
| A. | -$\frac{1}{2}$-$\frac{1}{3}$ | B. | -$\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$-$\frac{1}{3}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$ |
 如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( )
如图,⊙O中,直径CD⊥弦AB,则下列结论①△ABD是正△;②∠BOC=2∠ADC;③∠BOC=60°;④AC∥BD,正确的个数有( ) B.
B. 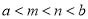
 D.
D. 