题目内容
8.1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$+…+$\frac{1}{1+2+3+…+10}$=$\frac{20}{11}$.分析 由于1+2+…+n=$\frac{n(n+1)}{2}$,那么$\frac{1}{1+2+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$),依此可得原式=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{10}$-$\frac{1}{11}$)=$\frac{20}{11}$.
解答 解:原式=2(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{10}$-$\frac{1}{11}$)
=2(1-$\frac{1}{11}$)
=$\frac{20}{11}$.
故答案为$\frac{20}{11}$.
点评 本题考查了规律型:数字的变化类,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.解决本题的难点在于找到规律:$\frac{1}{1+2+…+n}$=$\frac{2}{n(n+1)}$=2($\frac{1}{n}$-$\frac{1}{n+1}$).

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
17. 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )
 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA=( )| A. | 135° | B. | 125° | C. | 90° | D. | 60° |
3. 如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
 如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )
如图,PA、PB切⊙O于A、B两点,AC是⊙O的直径,∠P=40°,则∠ACB度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
20.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )
| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
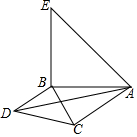 已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.
已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.
 如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.
如图,已知⊙O是四边形ABCD的外接圆,AB是⊙O的直径,BC=CD,过点C作PM⊥AD交AD的延长线于点M,交AB的延长线于点P.