题目内容
已知，如图，正方形DEFG内接于△ABC，AM⊥BC于M，交DG于N，BC=18，AM=12，求正方形的边长．考点：相似三角形的判定与性质,正方形的性质
专题：
分析：由DG∥BC得△ADG∽△ABC，利用相似三角形对应边上高的比等于相似比，列方程求解．
解答：解：设正方形的边长为x．
由正方形DEFG得，DG∥EF，即DG∥BC，
∵AH⊥BC，
∴AP⊥DG．
由DG∥BC得△ADG∽△ABC
∴
=
，
=
，
解得：x=
，
∴正方形的边长为：
．
由正方形DEFG得，DG∥EF，即DG∥BC，
∵AH⊥BC，
∴AP⊥DG．
由DG∥BC得△ADG∽△ABC
∴
| AN |
| AM |
| DG |
| BC |
| 12-x |
| 12 |
| x |
| 18 |
解得：x=
| 36 |
| 5 |
∴正方形的边长为：
| 36 |
| 5 |
点评：本题考查了相似三角形的判定与性质．关键是由平行线得到相似三角形，利用相似三角形的性质列方程．
练习册系列答案
名校课堂系列答案
相关题目
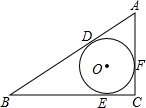如图，圆O是△ABC的内切圆，分别切AB，BC，CA于点D，E，F．设圆O的半径为r，BC=a，CA=b，AB=c，求证：S△ABC=
如图，在∠MON的两边上顺次取点，使 DE=CD=BC=AB=OA，若∠MON=20°，则∠NDE=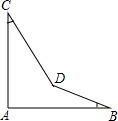
如图，∠A=90°，∠B=21°，∠C=32°，求∠BDC的度数．
一列快车从甲地开往乙地，一列慢车从乙地开往甲地，两车同时出发，车速不变，设慢车行驶t小时，两车相距S千米，S与t的关系如图所示，则慢车行驶