题目内容
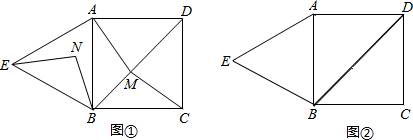
如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2.
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
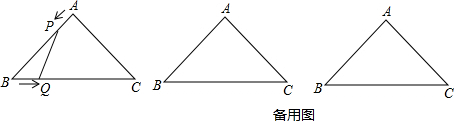
(1)当t为何值时,△PBQ是直角三角形?
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.

考点:相似形综合题,二次函数的最值,勾股定理,等腰直角三角形
专题:综合题
分析:(1)由于Rt△PBQ的直角不确定,需分∠BPQ=90°和∠BQP=90°两种情况讨论.由于∠B=45°,因此斜边是直角边的
倍,由此建立关于t的等量关系,就可解决问题.
(2)①过P作PH⊥BC,垂足为H,只需用t的代数式表示BQ和PH的长,就可得到y与t的函数关系式,根据条件容易得到t的取值范围;②根据二次函数的最值即可解决问题.
(3)过P作PH⊥BC,垂足为H,在Rt△PHQ中,根据勾股定理得到x与t之间的关系,代入y与t的函数关系式,即可得到y与x的函数关系式.
| 2 |
(2)①过P作PH⊥BC,垂足为H,只需用t的代数式表示BQ和PH的长,就可得到y与t的函数关系式,根据条件容易得到t的取值范围;②根据二次函数的最值即可解决问题.
(3)过P作PH⊥BC,垂足为H,在Rt△PHQ中,根据勾股定理得到x与t之间的关系,代入y与t的函数关系式,即可得到y与x的函数关系式.
解答:解:(1)由题可得:∠A=90°,AB=BC=4,∠B=45°,BQ=AP=t,BP=4-t.
①当∠PQB=90°时,如图1,
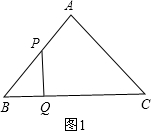
∵∠B=45°,
∴BQ=PQ.
∴BP=
=
BQ.
∴
t=4-t.
解得:t=
=4
-4.
②当∠BPQ=90°时,如图2,
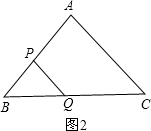
同理可得:BQ=
BP,∴
(4-t)=t
解得:t=
=8-4
.
综上所述;当t为(4
-4)秒或(8-4
)秒时,△PBQ是直角三角形.
(2)①过P作PH⊥BC,垂足为H,如图3,
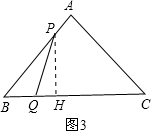
在Rt△PHB中,
同理可得:PH=
(4-t).
∴S△BPQ=
BQ•PH
=
(4-t)t
=-
t2+
t.
∴y=S△ABC-S△BPQ=8-(-
t2+
t)=
t2-
t+8.
由题意可知:0<t<4.
∴y与t的函数关系式为y=
t2-
t+8,0<t<4.
②y=
t2-
t+8=
(t-2)2+8-
.
∵
>0,
∴当t=2时,y取得最小值,最小值是8-
.
(3)如图3,

在Rt△PQH中,
∵PH=
(4-t),HQ=
(4-t)-t,PQ=x
∴x2=〔
(4-t)〕2+〔
(4-t)-t〕2
化简得:x2=(2+
)t2-4(2+
)t+16.
∴t2-4t=
.
∴y=
t2-
t+8=
(t2-4t)+8
=
×
+8
=
(x2-16)+8
=
x2-4
+12.
①当∠PQB=90°时,如图1,

∵∠B=45°,
∴BQ=PQ.
∴BP=
| BQ2+PQ2 |
| 2 |
∴
| 2 |
解得:t=
| 4 | ||
|
| 2 |
②当∠BPQ=90°时,如图2,

同理可得:BQ=
| 2 |
| 2 |
解得:t=
4
| ||
|
| 2 |
综上所述;当t为(4
| 2 |
| 2 |
(2)①过P作PH⊥BC,垂足为H,如图3,

在Rt△PHB中,
同理可得:PH=
| ||
| 2 |
∴S△BPQ=
| 1 |
| 2 |
=
| ||
| 4 |
=-
| ||
| 4 |
| 2 |
∴y=S△ABC-S△BPQ=8-(-
| ||
| 4 |
| 2 |
| ||
| 4 |
| 2 |
由题意可知:0<t<4.
∴y与t的函数关系式为y=
| ||
| 4 |
| 2 |
②y=
| ||
| 4 |
| 2 |
| ||
| 4 |
| 2 |
∵
| ||
| 4 |
∴当t=2时,y取得最小值,最小值是8-
| 2 |
(3)如图3,

在Rt△PQH中,
∵PH=
| 1 | ||
|
| 1 | ||
|
∴x2=〔
| 1 | ||
|
| 1 | ||
|
化简得:x2=(2+
| 2 |
| 2 |
∴t2-4t=
| x2-16 | ||
2+
|
∴y=
| ||
| 4 |
| 2 |
| ||
| 4 |
=
| ||
| 4 |
| x2-16 | ||
2+
|
=
| ||
| 4 |
=
| ||
| 4 |
| 2 |
点评:本题考查了等腰直角三角形的性质、二次函数的最值、勾股定理、解一元一次方程等知识,而第三小题中将t2-4t整体代换是解决该题的关键.

练习册系列答案
相关题目
 如图,已知△ABC和过点O的直线L.
如图,已知△ABC和过点O的直线L.
 如图,△A′B′C′是由△ABC沿射线AC方向平移得到,已知∠A=55°,∠B=60°,则∠C′=
如图,△A′B′C′是由△ABC沿射线AC方向平移得到,已知∠A=55°,∠B=60°,则∠C′=