题目内容
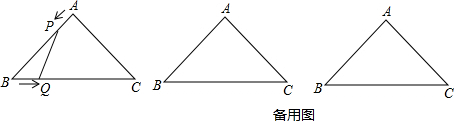
 如图,△A′B′C′是由△ABC沿射线AC方向平移得到,已知∠A=55°,∠B=60°,则∠C′=
如图,△A′B′C′是由△ABC沿射线AC方向平移得到,已知∠A=55°,∠B=60°,则∠C′=考点:平移的性质
专题:
分析:先根据三角形内角和定理求出∠ACB的度数,再由图形平移的性质得出△ABC≌△A′B′C′,根据全等三角形的性质即可得出结论.
解答:解:∵△ABC中,∠A=55°,∠B=60°,
∴∠ACB=180°-60°-55°=65°,
∵△A′B′C′是由△ABC沿射线AC方向平移得到,
∴△ABC≌△A′B′C′,
∴∠C′=∠ACB=65°.
故答案为:65.
∴∠ACB=180°-60°-55°=65°,
∵△A′B′C′是由△ABC沿射线AC方向平移得到,
∴△ABC≌△A′B′C′,
∴∠C′=∠ACB=65°.
故答案为:65.
点评:本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.

练习册系列答案
相关题目
在下列图形中,既是轴对称图形,又是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,D是BC延长线上一点,∠ACD=120°,∠B=40°,则∠A的度数是
如图,在△ABC中,D是BC延长线上一点,∠ACD=120°,∠B=40°,则∠A的度数是 如图,直线AB、CD被直线EF所截,则∠1的内错角是
如图,直线AB、CD被直线EF所截,则∠1的内错角是 如图,已知:在△ABC中,AB<AC,BC边上的垂直平分线DE交BC于点D,交AC于点E,AC=8,△ABE的周长是14,AB的长是
如图,已知:在△ABC中,AB<AC,BC边上的垂直平分线DE交BC于点D,交AC于点E,AC=8,△ABE的周长是14,AB的长是