题目内容
一个无盖纸盒,底面是面积为100平方厘米的正方形,高是15厘米,小丽把一根木棒放在纸盒中,量得木棒露出纸盒外面部分是2厘米,请求出这根木棒的总长度的取值范围.
考点:勾股定理的应用
专题:
分析:根据正方形的面积公式求得正方形的边长,再进一步求得正方形的对角线的平方,根据勾股定理进而求得纸盒内部的木棒长,从而求得木棒的总长.
解答: 解:如图所示:
解:如图所示:
根据正方形的面积公式,得底面正方形的边长是10cm,则其对角线为:10
cm,
根据勾股定理进一步求得纸盒内部的木棒的长度是
=5
.
则木棒的总长为:5
+2(cm),
当木棒垂直底面则总长度度为:15+2=17(cm),
故这根木棒的总长度x的取值范围是:17≤x≤5
+2.
 解:如图所示:
解:如图所示:根据正方形的面积公式,得底面正方形的边长是10cm,则其对角线为:10
| 2 |
根据勾股定理进一步求得纸盒内部的木棒的长度是
(10
|
| 17 |
则木棒的总长为:5
| 17 |
当木棒垂直底面则总长度度为:15+2=17(cm),
故这根木棒的总长度x的取值范围是:17≤x≤5
| 17 |
点评:此题主要考查了勾股定理的应用,利用勾股定理结合分类讨论得出是解题关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
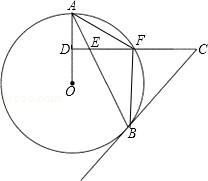 如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连结AF、BF.
如图,AB是⊙O的弦,D为OA半径的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB.连结AF、BF. 已知:如图,在矩形ABCD中,点E在CD上,BF⊥AE,垂足为F,AE2=AD•AB.求证:AE=BF.
已知:如图,在矩形ABCD中,点E在CD上,BF⊥AE,垂足为F,AE2=AD•AB.求证:AE=BF. 如图所示,已知△ABC中,∠BAC=90°,AB=AC,E是AC的中点,CD⊥AC,ED交BC于F.若CD=AB,求证:AF⊥BE.
如图所示,已知△ABC中,∠BAC=90°,AB=AC,E是AC的中点,CD⊥AC,ED交BC于F.若CD=AB,求证:AF⊥BE. 如图,在等腰三角形ABC中,AB=AC,两底角的平分线BE、CD相交于点O.
如图,在等腰三角形ABC中,AB=AC,两底角的平分线BE、CD相交于点O. 如图,BC与AB的比为黄金比,这样的矩形称为黄金矩形,他给人以美感,某建筑物的窗户为黄金矩形,已知他的一边长为3.24m.求它的邻边长(精确到0.01m)
如图,BC与AB的比为黄金比,这样的矩形称为黄金矩形,他给人以美感,某建筑物的窗户为黄金矩形,已知他的一边长为3.24m.求它的邻边长(精确到0.01m)