题目内容
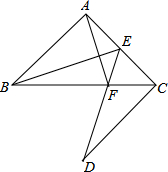 如图所示,已知△ABC中,∠BAC=90°,AB=AC,E是AC的中点,CD⊥AC,ED交BC于F.若CD=AB,求证:AF⊥BE.
如图所示,已知△ABC中,∠BAC=90°,AB=AC,E是AC的中点,CD⊥AC,ED交BC于F.若CD=AB,求证:AF⊥BE.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:易证△ABE≌△CDE,△ACF≌△DCF,即可得∠ABE=∠CDE,∠CDE=∠CAF,根据∠ABE+∠AEB=90°即可求得∠AHE=90°,即可解题.
解答:解:如图,
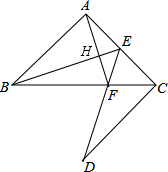
在△ABE和△CDE中,
,
∴△ABE≌△CDE(SAS),
∴∠ABE=∠CDE,
∵AB=AC,∠BAC=90°,
∴∠ACF=45°,
∴∠DCF=45°,
在△ACF和△DCF中,
,
∴△ACF≌△DCF(SAS)
∴∠CAF=∠CDF,
∴∠CAF=∠ABE,
∵∠ABE+∠AEB=90°,
∴∠CAF+∠AEB=90°,
∴∠AHE=90°.

在△ABE和△CDE中,
|
∴△ABE≌△CDE(SAS),
∴∠ABE=∠CDE,
∵AB=AC,∠BAC=90°,
∴∠ACF=45°,
∴∠DCF=45°,
在△ACF和△DCF中,
|
∴△ACF≌△DCF(SAS)
∴∠CAF=∠CDF,
∴∠CAF=∠ABE,
∵∠ABE+∠AEB=90°,
∴∠CAF+∠AEB=90°,
∴∠AHE=90°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABE≌△CDE和△ACF≌△DCF是解题的关键.

练习册系列答案
相关题目
已知点A(-2,1),点B(3,2),在x轴上求一点P,使AP+BP最小,下列作法正确的是( )
| A、点P与O(0.0)重合 |
| B、连接AB交y轴于P,点P即为所求. |
| C、过点A作x轴的垂线,垂足为P,点P即为所求 |
| D、作点B关于x轴的对称点C,连接AC,交x轴于P,点P即为所求 |
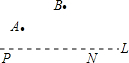 某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短?
某市计划在一条公路L上修建一个火车站P和一个汽车站N,且使两站相距2km,在公路的一侧有景点A,B.如图所示旅客从P站坐车到两处游玩后,直接到N站坐汽车回到P站,则当P站修在公路何处时,能使旅客所走路程最短? 如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证:
如图,已知正方形ABCD与正方形CEFG,点G在边CD上,连接AF,取AF中点M,连接DM、GM.求证: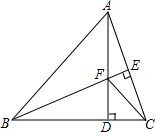 如图△ABC中,AB=BC,BC⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE相交于点F,连接CF.
如图△ABC中,AB=BC,BC⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE相交于点F,连接CF. 如图所示,Rt△ABC中有一个正方形BDEF,已知图中阴影部分的面积为27cm2,AF+DC=12cm,那么△ABC的面积是多少平方厘米?
如图所示,Rt△ABC中有一个正方形BDEF,已知图中阴影部分的面积为27cm2,AF+DC=12cm,那么△ABC的面积是多少平方厘米?