题目内容
已知x、y满足关系式（x-2）2+|2x-5y-2a|=0，且y为正数，求a的取值范围．
考点：非负数的性质：偶次方,非负数的性质：绝对值,解一元一次不等式
专题：
分析：利用偶次方的性质结合绝对值的性质表示出y的值，进而求出a的取值范围．
解答：解：∵（x-2）2+|2x-5y-2a|=0，且y为正数，
∴
，
解得：
，
∵y为正数，
∴a的取值范围是：a＜2．
∴
|
解得：
|
∵y为正数，
∴a的取值范围是：a＜2．
点评：此题主要考查了偶次方的性质结合绝对值的性质以及解不等式，表示出y的值是解题关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
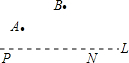某市计划在一条公路L上修建一个火车站P和一个汽车站N，且使两站相距2km，在公路的一侧有景点A，B．如图所示旅客从P站坐车到两处游玩后，直接到N站坐汽车回到P站，则当P站修在公路何处时，能使旅客所走路程最短？在△ABC和△DEF中，若AB=FD，BC=DE，CA=EF，则（ ）
| A、△ABC≌△DEF |
| B、△ABC≌△EDF |
| C、△ABC≌△DFE |
| D、△ABC≌△FDE |