题目内容
已知：如图，在矩形ABCD中，点E在CD上，BF⊥AE，垂足为F，AE2=AD•AB．求证：AE=BF．考点：相似三角形的判定与性质
专题：证明题
分析：利用条件可证明△ABF∽△EAD，可得AE•BF=AD•AB，结合AE2=AD•AB，可得AE=BF．
解答：证明：
∵四边形ABCD为矩形，
∴∠D=90°，DE∥AB，
∴∠BAF=∠DEA，
∴BF⊥AE，
∴∠BFA=∠D，
∴△ABF∽△EAD，
∴
=
，
∴AE•BF=AD•AB，
又AE2=AD•AB，
∴AE2=AE•BF，且AE≠0，
∴AE=BF．
∵四边形ABCD为矩形，
∴∠D=90°，DE∥AB，
∴∠BAF=∠DEA，
∴BF⊥AE，
∴∠BFA=∠D，
∴△ABF∽△EAD，
∴
| AB |
| AE |
| BF |
| AD |
∴AE•BF=AD•AB，
又AE2=AD•AB，
∴AE2=AE•BF，且AE≠0，
∴AE=BF．
点评：本题主要考查相似三角形的判定和性质，掌握三角形相似的判定是解题的关键．注意利用相似三角形也可以证明线段相等．
练习册系列答案
相关题目
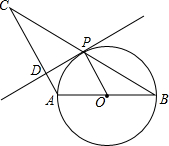如图，△ABC中，AB=AC，以AB为直径的圆O交BC于点P，PD⊥AC于点D
如图，在角坐标系中，射线Ox绕原点O逆时针旋转300°到OP的位置，若OP=2，则点P的坐标为