Question

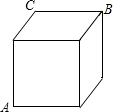在一个棱长为3cm的立方体纸箱的A点有一只蜘蛛看见一只蚂蚁从纸箱B点沿BC往C点爬行，如果蚂蚁的爬行速度为1cm/s，蜘蛛的爬行速度为2cm/s，请你分析一下，蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是多少秒？

Answer 1

考点：平面展开-最短路径问题

专题：

分析：利用已知画出展开图，进而利用勾股定理求出相遇的时间，即可得出答案．

解答：解：如图所示：
设x秒时在B′点蜘蛛捉住蚂蚁，
在Rt△ACB′中，AC²+B′C²=AB′²，
则BB′=（3-x）cm，AB′=2xcm，
故6²+（3-x）²=（2x）²
解得：x₁=3，x₂=-5（不合题意舍去），
即在C点正好捉到蚂蚁，
答：蜘蛛沿纸箱表面爬去捉住蚂蚁的最短时间是3秒．

点评：此题主要考查了平面展开图最短路径问题，利用勾股定理得出是解题关键．