题目内容
 求证:等腰三角形两腰上的中线相等.
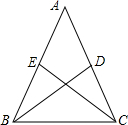
求证:等腰三角形两腰上的中线相等.已知:如图,△ABC中,AB=AC,BD、CE分别为△ABC的中线.
求证:
证明:∵BD、CE分别为△ABC的中线
∴AE=
| 1 |
| 2 |
∵AB=AC∴
在△ABD与△ACE中
|
①
∴△ABD≌△ACE (
∴BD=CE.
考点:等腰三角形的性质,全等三角形的判定与性质
专题:推理填空题
分析:根据已知画出图形,易证△ABD≌△ACE,根据全等三角形的性质,得BD=CE.
解答:解:如图,△ABC中,AB=AC,BD、CE分别为△ABC的中线.
求证:BD=CE.
证明:∵BD、CE分别为△ABC的中线,
∴AE=
AB,AD=
AC,
∵AB=AC,
∴AD=AE,
在△ABD与△ACE中
,
①∠A=∠A,②AB=AC,
∴△ABD≌△ACE( SAS),
∴BD=CE.
故答案为:BD=CE;
AC;AD=AE;∠A=∠A,AB=AC;SAS.
求证:BD=CE.
证明:∵BD、CE分别为△ABC的中线,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴AD=AE,
在△ABD与△ACE中
|
①∠A=∠A,②AB=AC,
∴△ABD≌△ACE( SAS),
∴BD=CE.
故答案为:BD=CE;
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质及等腰三角形的性质;证明的步骤是:先根据题意画出图形,再根据图形写出已知和求证,最后写出证明过程.

练习册系列答案
相关题目
 反比例函数y=
反比例函数y=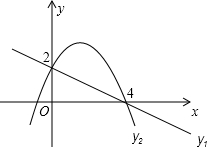 如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)
如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)