题目内容
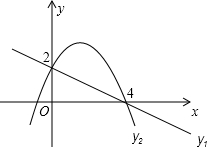 如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)
如图,已知直线y1=kx+b1与抛物线y2=-x2+b2x+c都经过点(4,0)和(0,2)(1)求直线和抛物线解析式;
(2)当y1>y2,求x的取值范围.
考点:待定系数法求二次函数解析式,二次函数与不等式(组)
专题:计算题
分析:(1)将已知两点坐标代入直线与抛物线解析式求出各字母的值,即可确定出各自的解析式;
(2)由函数图象找出满足题意x的范围即可.
(2)由函数图象找出满足题意x的范围即可.
解答:解:(1)将(4,0)与(0,2)分别代入直线解析式得:
,
解得:k=-
,b1=2,即直线解析式为y1=-
x+2;
将(4,0)与(0,2)分别代入抛物线解析式得:
,
解得:b2=3.5,c=2,即抛物线解析式为y2=-x2+3.5x+2;
(2)根据两函数交点坐标为(0,2),(4,0),
由图象得:当y1>y2时,x的取值范围为x<2或x>4.
|
解得:k=-
| 1 |
| 2 |
| 1 |
| 2 |
将(4,0)与(0,2)分别代入抛物线解析式得:
|
解得:b2=3.5,c=2,即抛物线解析式为y2=-x2+3.5x+2;
(2)根据两函数交点坐标为(0,2),(4,0),
由图象得:当y1>y2时,x的取值范围为x<2或x>4.
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

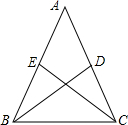 求证:等腰三角形两腰上的中线相等.
求证:等腰三角形两腰上的中线相等.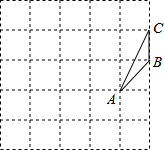 如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?
如图,由边长为1的25个小正方形组成的正方形网络上有一个三角形ABC;在网络上画一个与三角形ABC相似的且面积最大的三角形,使它的三个顶点都落在小正方形的顶点上,并请你算一算,这个三角形的最大面积是多少?