题目内容
已知x=1是方程
-
=x-1的一个根,求a的值以及方程的另一个根.
| x2+3ax-7 |
| x2+x-a |
考点:无理方程
专题:
分析:首先将x=1代入求出a的值,进而利用x-1的取值范围进而求出方程的另一个根.
解答:解:把x=1代入方程得:
-
=0,
即
=
,
两边平方,得:3a-6=2-a,
解得:a=2.
检验:a=2满足方程
-
=0.
把a=2代入原方程,得:
-
=x-1.
即:(
-
)2=(x-1)2,
(x-1)(x+7)+(x-1)(x+2)-2
×
=(x-1)2
当x-1>0时
(x+7)+(x+2)-2
=x-1
x+10=2
,
两边平方得:
3x2+16x-44=0,
解得:x1=2,x2=-
(不合题意舍去),
当x-1<0时,则x+2<0,x+7<0,
故x<-7,
(x+7)+(x+2)+2
=1-x
-3x-8=2
,
两边平方得:
5x2+12x+8=0,
此方程无解.
故方程的另一个根为2.
| 1+3a-7 |
| 1+1-a |
即
| 3a-6 |
| 2-a |
两边平方,得:3a-6=2-a,
解得:a=2.
检验:a=2满足方程
| 1+3a-7 |
| 1+1-a |
把a=2代入原方程,得:
| x2+6x-7 |
| x2+x-2 |
即:(
| x2+6x-7 |
| x2+x-2 |
(x-1)(x+7)+(x-1)(x+2)-2
| (x-1)(x+7) |
| (x-1)(x+2) |
当x-1>0时
(x+7)+(x+2)-2
| (x+2)(x+7) |
x+10=2
| (x+2)(x+7) |
两边平方得:
3x2+16x-44=0,
解得:x1=2,x2=-
| 22 |
| 3 |
当x-1<0时,则x+2<0,x+7<0,
故x<-7,
(x+7)+(x+2)+2
| (x+2)(x+7) |
-3x-8=2
| (x+2)(x+7) |
两边平方得:
5x2+12x+8=0,
此方程无解.
故方程的另一个根为2.
点评:此题主要考查了无理方程的解法,熟练利用完全平方公式解方程是解题关键.

练习册系列答案
相关题目
要使式子
-
+3有意义,则x的取值范围为( )
| 1-x |
| x+1 |
| A、-1≤x≤0 | B、-1≤x≤1 |
| C、x≤1 | D、x≤-1 |

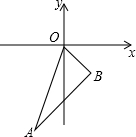 如图,直线OA的解析式为y=3x,点A的横坐标是-1,OB=
如图,直线OA的解析式为y=3x,点A的横坐标是-1,OB=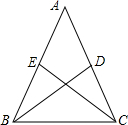 求证:等腰三角形两腰上的中线相等.
求证:等腰三角形两腰上的中线相等.