题目内容
14.计算与化简(1)$\frac{\sqrt{15}+\sqrt{60}}{\sqrt{3}}$-3$\sqrt{5}$
(2)3$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$
(3)$\sqrt{16}$+$\root{3}{-27}$+3$\sqrt{3}$-$\sqrt{(-3)^{2}}$
(4)(π-2009)0+$\sqrt{12}$+|$\sqrt{3}$-2|
分析 (1)原式利用二次根式的除法法则计算,合并即可得到结果;
(2)原式各项化简后,合并即可得到结果;
(3)原式利用算术平方根,立方根定义计算,合并即可得到结果;
(4)原式利用零指数幂法则,绝对值的代数意义化简,合并即可得到结果.
解答 解:(1)原式=$\sqrt{5}$+$\sqrt{20}$-3$\sqrt{5}$=$\sqrt{5}$+2$\sqrt{5}$-3$\sqrt{5}$=0;
(2)原式=9$\sqrt{2}$+$\sqrt{2}$-2$\sqrt{2}$=8$\sqrt{2}$;
(3)原式=4-3+3$\sqrt{3}$-3=3$\sqrt{3}$-2;
(4)原式=1+2$\sqrt{3}$+2-$\sqrt{3}$=3+$\sqrt{3}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
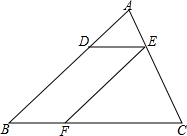 如图,在△ABC中,AB=3AD,DE∥BC,EF∥AB,AB=BC=9,AC=6.
如图,在△ABC中,AB=3AD,DE∥BC,EF∥AB,AB=BC=9,AC=6. 如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2.
如图所示,在等腰梯形ABCD中,AB∥CD,AC⊥BD,AC=6cm,则等腰梯形ABCD的面积是18cm2.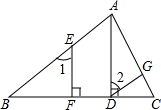 如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:∠B=∠GDC.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:∠B=∠GDC.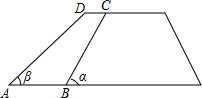 如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.
如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.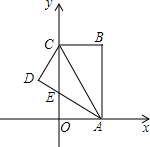 如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.
如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.