题目内容
15.解方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$时,一学生把c看错而得$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$,而正确的解是$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,那么a、b、c的值是( )| A. | 不能确定 | B. | 4,5,-2 | C. | 4,7,2 | D. | 4,7,-2 |
分析 把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得出3a-2b=2,3c-7×(-2)=8,-2a+2b=2,求得c,建立a、b的方程组求得a、b即可.
解答 解:$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-2}\\{y=2}\end{array}\right.$代入方程组$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得
3a-2b=2,3c-7×(-2)=8,-2a+2b=2,
因此c=-2,$\left\{\begin{array}{l}{3a-2b=2}\\{-2a+2b=2}\end{array}\right.$,
解得:a=4,b=5,c=-2.
故选:B.
点评 此题主要考查了二元一次方程组的解,掌握解二元一次方程组的方法是解决问题的关键.

练习册系列答案
相关题目
7.若(-7x2-5y)( )=49x4-25y2,括号内应填代数式( )
| A. | 7x2+5y | B. | -7x2-5y | C. | -7x2+5y | D. | 7x2-5y |
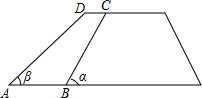 如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.
如图,沿水库拦水坝的背水坡将坝面加宽CD=2米,坡度由原来的$\sqrt{3}$:1改为1:1,已知背水坡BC长12米.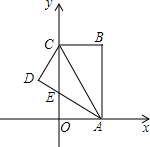 如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.
如图,长方形AB长为9,OA长为3,将长方形沿对角线AC折叠,使得点B与点D重合,且与y轴交于点E.