题目内容
11.在一个不透明的袋子中装有 红,绿,蓝3种颜色的球共10个,这些球除颜色外都相同,其中红球3个,绿球5个.任意摸出2个球恰好为同色球的概率是$\frac{14}{45}$.分析 列表得出所有等可能结果,根据概率公式计算可得.
解答 解:列表如下:
| 红1 | 红2 | 红3 | 绿1 | 绿2 | 绿3 | 绿4 | 绿5 | 蓝1 | 蓝2 | |
| 红1 | 红、红 | 红、红 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、蓝 | 红、蓝 | |
| 红2 | 红、红 | 红、红 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、蓝 | 红、蓝 | |
| 红3 | 红、红 | 红、红 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、绿 | 红、蓝 | 红、蓝 | |
| 绿1 | 绿、红 | 绿、红 | 绿、红 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、蓝 | 绿、蓝 | |
| 绿2 | 绿、红 | 绿、红 | 绿、红 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、蓝 | 绿、蓝 | |
| 绿3 | 绿、红 | 绿、红 | 绿、红 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、蓝 | 绿、蓝 | |
| 绿4 | 绿、红 | 绿、红 | 绿、红 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、蓝 | 绿、蓝 | |
| 绿5 | 绿、红 | 绿、红 | 绿、红 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、绿 | 绿、蓝 | 绿、蓝 | |
| 蓝1 | 蓝、红 | 蓝、红 | 蓝、红 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、蓝 | |
| 蓝2 | 蓝、红 | 蓝、红 | 蓝、红 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、绿 | 蓝、蓝 |
∴P(摸出2个球恰好为同色球)=$\frac{28}{90}$=$\frac{14}{45}$,
故答案为:$\frac{14}{45}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.一只青蛙在水井底,每天向上跃4m,又滑下3m,若井深9m,则它跃上这口井一共需( )
| A. | 8天 | B. | 7天 | C. | 6天 | D. | 5天 |
 如图,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$.写出新距形各顶点的坐标.
如图,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$.写出新距形各顶点的坐标.
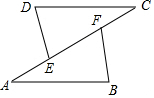 如图,点E,F在AC上,AB=CD,AE=CF,BF=DE,△ABF与△CDE全等吗?说明你的理由.
如图,点E,F在AC上,AB=CD,AE=CF,BF=DE,△ABF与△CDE全等吗?说明你的理由.