题目内容
20.我们把不相等的两个实数a,b中较大实数a记作max{a,b}=a,例如:max{2.3,3.4}=3.4,max{-5.6,-8.7}=-5.6,max{-3,0}=0…那么:关于x的方程$max\left\{{x,-x}\right\}=\frac{2x+1}{x}$的解是-1或$1+\sqrt{2}$.
分析 根据新定义分x>-x、-x>x两种情况,分别列出方程求解即可.
解答 解:①当x>-x,即x>0时,有:x=$\frac{2x+1}{x}$,
解得:x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$(舍);
②当-x>x,即x<0时,有-x=$\frac{2x+1}{x}$,
解得:x=-1;
综上,关于x的方程$max\left\{{x,-x}\right\}=\frac{2x+1}{x}$的解是x=1+$\sqrt{2}$或x=-1.
故答案为:-1或$1+\sqrt{2}$.
点评 本题主要考查对新定义的理解及解分式方程的能力,由新定义会分类讨论是前提,准确解分式方程及方程的解的取舍是关键.

练习册系列答案
相关题目
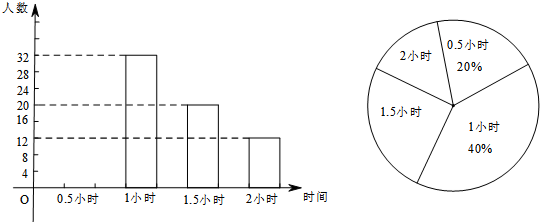
10. 根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
(1)计算各项目的百分比并填写在表格中;
(2)计算各项目对应的扇形圆心角,并填写在表格中;
(3)利用给出的圆画出扇形统计图.
 根据下表所列数据,制作扇形统计图表示小明一天的时间安排:
根据下表所列数据,制作扇形统计图表示小明一天的时间安排:| 项目 | 时间/h | 所占的百分比 | 对应的扇形圆心角的度数 |
| 睡觉 | 9 | ||
| 活动 | 4 | ||
| 学习 | 8 | ||
| 吃饭 | 1 | ||
| 其他 | 2 |
(2)计算各项目对应的扇形圆心角,并填写在表格中;
(3)利用给出的圆画出扇形统计图.
9. 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
 如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )
如图,直线AB∥CD,AC⊥BC于点C,若∠1=40°,则∠2的度数是( )| A. | 50° | B. | 40° | C. | 80° | D. | 60° |
 如图,已知a∥b,如果∠1=52°,那么∠2=52°,∠3=128°,∠4=52°.
如图,已知a∥b,如果∠1=52°,那么∠2=52°,∠3=128°,∠4=52°.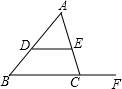 如图,DE∥BC,CF为BC的延长线,若∠ADE=50°,∠ACF=110°,则∠A=60°.
如图,DE∥BC,CF为BC的延长线,若∠ADE=50°,∠ACF=110°,则∠A=60°.