题目内容
12.在平面直角坐标系中描出下列各点.并将各点用线段顺次连接起来.A(-2,3),B(2,3),C(5,0),D(-2,0)
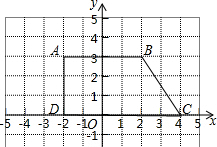
(1)图形中,线段CD上的点都在x轴上,它们的坐标特点是纵坐标为0;
(2)A、D两点横坐标相等,线段AD平行于y轴;
(3)线段AB与CD的位量关系是垂直;
(4)描出的图形梯形,它的面积为15.
分析 (1)由x轴上点的坐标特点即可得出结论;
(2)由A、D两点横坐标相等,得出AD⊥x轴,即可得出结论;
(3)由AD⊥x轴,得出AD⊥CD即可;
(4)根据题意得出AB=4,AD=3,CD=6,由梯形ABCD的面积公式即可得出结果.
解答 解:(1)∵线段CD上的点都在x轴上,
∴它们的坐标特点是纵坐标为0;
故答案为:纵坐标为0;
(2)∵A、D两点横坐标相等,
∴AD⊥x轴,
∴线段AD∥y轴;
故答案为:y轴;
(3)∵AD⊥x轴,线段CD上的点都在x轴上,
∴AD⊥CD;
故答案为:垂直;
(4)根据题意得:AB=4,AD=3,CD=6,
∴梯形ABCD的面积=$\frac{1}{2}$(4+6)×3=15;
故答案为:15.
点评 本题考查了梯形的性质、坐标与图形性质、梯形面积的计算;熟练掌握梯形的性质和坐标与图形性质是解决问题的关键.

练习册系列答案
相关题目
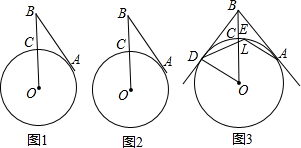
 如图,图中的三角形共有3个,∠C的对边是AD或AB.
如图,图中的三角形共有3个,∠C的对边是AD或AB.