题目内容
如图，以AB为直径的半圆绕A点，逆时针旋转60°，点B旋转到点B′的位置，已知AB=6，则图中阴影部分的面积为（ ）| A、6π | B、5π | C、4π | D、3π |
考点：旋转的性质,扇形面积的计算
专题：
分析：根据旋转的性质得出阴影部分的面积为：S扇形B′AB进而利用扇形面积公式求出即可．
解答：解：如图所示：∵以AB为直径的半圆绕A点，逆时针旋转60°，
∴AB=AB′=6，∠BAB′=60°，
∴图中阴影部分的面积为：S扇形B′AB=
=6π．
故选：A．
∴AB=AB′=6，∠BAB′=60°，
∴图中阴影部分的面积为：S扇形B′AB=
| 60π×62 |
| 360 |
故选：A．
点评：此题主要考查了扇形面积公式以及旋转的性质，得出阴影部分的面积=S扇形B′AB是解题关键．
练习册系列答案
相关题目
如图，直线AB∥CD，AF交CD于点E，∠BED=30°，∠AEB=80°，则A=如图，直线l上有2个圆点A、B，我们进行如下操作：第1次操作，在A、B两圆点间插入一个圆点C，这时直线l上有（2+1）个圆点；第2次操作，在A、C和C、B间再分别插入一个圆点，这时直线l上有（3+2）个圆点；第3次操作，在每相邻的两圆点间再插入一个圆点，这时直线l上有（5+4）个圆点；…第7次操作时，插入的圆点个数为（ ）
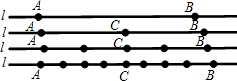
| A、129 | B、22 | C、32 | D、65 |
在平面内，⊙O的半径为2cm，圆心O到直线l的距离为3cm，则直线l与⊙O的位置关系是（ ）
| A、内含 | B、相交 | C、相切 | D、相离 |
当x=-2时，代数式x2-5的值为（ ）
| A、-9 | B、-3 | C、-1 | D、2 |
如图，AB与CD交于点O，OE平分∠COB，BF∥OE，已知∠BOD=20°，则∠ABF=（ ）| A、100° | B、110° |
| C、120° | D、140° |