题目内容
我们容易发现,反比例函数y=
的图象既是一个轴对称图形,又是一个中心对称图形,我们可以利用这些性质解决问题.
(1)①反比例函数y=
图象有 条对称轴,直线方程分别为 ;反比例函数y=
图象的对称中心坐标为 ;
②如果反比例函数y=
的图象经过点(a,b),那么它一定同时经过点 ;(用字母a,b表示,写出两个即可)
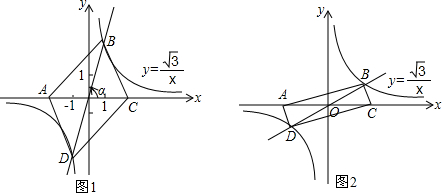
(2)如图1,直线y=nx与反比例函数y=
的图象分别交于第一、三象限的点B、D,已知点A(-m,0),C(m,0)
①判断四边形ABCD的形状,并证明你的结论;
②当点B为(p,1)时,四边形ABCD是矩形,如图2,试求p和m的值.
| k |
| x |
(1)①反比例函数y=
| k |
| x |
| k |
| x |
②如果反比例函数y=
| k |
| x |
(2)如图1,直线y=nx与反比例函数y=
| ||
| x |
①判断四边形ABCD的形状,并证明你的结论;
②当点B为(p,1)时,四边形ABCD是矩形,如图2,试求p和m的值.

考点:反比例函数综合题
专题:
分析:(1)①直接根据反比例函数的对称性进行解答即可;
②根据反比例函数的图象既是一个轴对称图形,又是一个中心对称图形解答;
(2)①根据反比例函数y=
是中心对称图形,且与正比例函数y=nx交与点B、D可知OB=OD,再根据A(-m,0),C(m,0)可知OA=OC,由此可得出结论;
②把点B(p,1)代入y=
即可求出p的值,过点B作BE⊥x轴于点E,则OE=
,BE=1,在Rt△OBE中,由勾股定理求出OB的长,四边形ABCD是矩形,且C(m,0)可得出OB=OC,进而得出m的值.
②根据反比例函数的图象既是一个轴对称图形,又是一个中心对称图形解答;
(2)①根据反比例函数y=
| ||
| x |
②把点B(p,1)代入y=
| ||
| x |
| 3 |
解答: 解:(1)①反比例函数y=
解:(1)①反比例函数y=
图象有2条对称轴,直线方程分别为直线y=x,直线y=-x;反比例函数y=
图象的对称中心坐标为 (0,0),
故答案为:2,直线y=x,直线y=-x,(0,0);
②∵反比例函数y=
的图象既是一个轴对称图形,又是一个中心对称图形,
∴如果反比例函数y=
的图象经过点(a,b),那么它一定同时经过点(-a,-b)或(b,a)或(-b,-a).
故答案为:(-a,-b)或(b,a)或(-b,-a);
(2)①四边形ABCD是平行四边形.
证明:∵反比例函数y=
是中心对称图形,且与正比例函数y=nx交与点B、D,
∴OB=OD,
∵A(-m,0),C(m,0),
∴OA=OC,
∴四边形ABCD是平行四边形;
②∵点B(p,1)在y=
的图象上,
∴1=
,
∴p=
,
过点B作BE⊥x轴于点E,则OE=
,BE=1,
在Rt△OBE中,由勾股定理得,OB=
=2,
∵四边形ABCD是矩形,且C(m,0),
∴OB=OC=2,
∴m=2.
 解:(1)①反比例函数y=
解:(1)①反比例函数y=| k |
| x |
| k |
| x |
故答案为:2,直线y=x,直线y=-x,(0,0);
②∵反比例函数y=
| k |
| x |
∴如果反比例函数y=
| k |
| x |
故答案为:(-a,-b)或(b,a)或(-b,-a);
(2)①四边形ABCD是平行四边形.
证明:∵反比例函数y=
| ||
| x |
∴OB=OD,
∵A(-m,0),C(m,0),
∴OA=OC,
∴四边形ABCD是平行四边形;
②∵点B(p,1)在y=
| ||
| x |
∴1=
| ||
| p |
∴p=
| 3 |
过点B作BE⊥x轴于点E,则OE=
| 3 |
在Rt△OBE中,由勾股定理得,OB=
(
|
∵四边形ABCD是矩形,且C(m,0),
∴OB=OC=2,
∴m=2.
点评:本题考查的是反比例函数综合题,涉及到平行四边形的判定定理、反比例函数的性质等知识,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x=2是关于x的方程x-2a=0的解,则a的值为( )
| A、4 | B、3 | C、1 | D、2 |
用反证法证明“在同一平面内,若a⊥b,a⊥c,则b∥c时,第一步应假设( )
| A、b不平行c | B、a不垂直c |
| C、a不垂直b | D、b∥c |
下列计算中,正确的是( )
| A、a4•a3=a12 |
| B、(x2)3=x5 |
| C、(2x3)2=4x6 |
| D、b5+b5=2b10 |
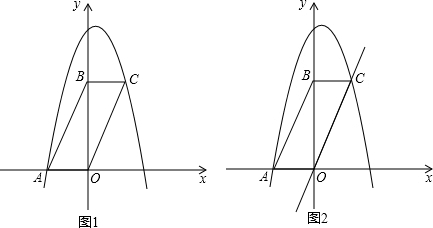
 用直尺作图:如图△ABC中AB=AC,四边形BCDE为矩形,请只用直尺作出BC的垂直平分线.
用直尺作图:如图△ABC中AB=AC,四边形BCDE为矩形,请只用直尺作出BC的垂直平分线. 如图:在?ABCD中,AC为其对角线,过点D作AC的平行线与BC的延长线交于E.
如图:在?ABCD中,AC为其对角线,过点D作AC的平行线与BC的延长线交于E.